Álgebra Linear para Computação Quântica#
Nota
Material extraído do TCC Computação Quântica: Uma abordagem para estudantes de graduação em Ciências Exatas, de Giovani Goraiebe Pollachini.
NESTE capítulo, um resumo de Álgebra Linear voltado para Computação Quântica é apresentado. A teoria é apresentada usando-se a notação de Dirac, ou, notação de braket, uma notação utilizada largamente em Mecânica Quântica e que será necessária para o restante do trabalho. Essa notação é conveniente para se fazer contas e faz com que as diversas operações possíveis se encaixem naturalmente.
Na Álgebra Linear abstrata, pode-se considerar espaços vetoriais sobre diversos corpos (ou escalares), que são estruturas algébricas com propriedades semelhantes aos números reais e complexos. Os espaços vetoriais podem ter dimensão finita ou infinita.
Na Computação Quântica o interesse é voltado a espaços vetoriais de dimensão finita sobre o corpo dos números complexos. Isso permite a identificação do espaço com as \(n\)-uplas de números complexos, o que simplifica grandemente a teoria. Os resultados resumidos neste capítulo estão situados nesse contexto.
A principal referência para esse capítulo é [NC10]. Outra referência muito útil é [Lim21], que possui um capítulo voltado a espaços vetoriais complexos. Livros texto clássicos de Álgebra Linear, como [SW09] também são úteis. Embora tenham ênfase em espaços vetoriais reais, a maioria das definições, resultados e demonstrações se transporta integralmente para os espaços vetoriais complexos.
Será considerado um pré-requisito a este texto um curso de Álgebra Linear ao nível de graduação abordando-se os seguintes itens: espaços vetoriais, base e dimensão, transformações lineares, autovalores e autovetores. Por ter um caráter de resumo, os resultados apresentados, via de regra, não são acompanhados de suas demonstrações, as quais podem ser encontradas nos livros mencionados no parágrafo anterior.
Espaço Vetorial, Base e Dimensão#
Espaço Vetorial#
O conjunto das \(n\)-uplas \((z_0, \ldots, z_{n-1})\) de números complexos com a soma e o produto por escalar definidos entrada a entrada é um Espaço Vetorial Complexo e é denotado por \(\mathbb{C}^n\). É conveniente representar esses elementos por vetores coluna. Tem-se então:
Em Mecânica Quântica, os vetores de \(\mathbb{C}^n\) costumam ser usados na notação de Dirac, ou notação de braket:
Um vetor \(\ket{\psi}\) é chamado ket (em contraponto com \(\bra{\psi}\), que será definido posteriormente, e será chamado bra).
Os vetores se comportam de maneira semelhante aos números no que diz respeito à soma e subtração. Em particular, a soma comuta \(\ket{\phi} + \ket{\psi} = \ket{\psi} + \ket{\phi}\), há um vetor nulo, denotado por \(0\) ou \(\ket{\varnothing} = (0, \ldots , 0)\) de tal forma que \(\ket{\psi} + 0 = \ket{\psi}\) e, ainda, vale \(-\ket{\psi} = (-z_0, \dots , -z_{n-1}) = -1 \cdot \ket{\psi}\). O produto por escalar também se comporta de maneira semelhante ao produto numérico, e valem as propriedades distributivas \(z(\ket{\phi} + \ket{\psi}) = z \ket{\phi} + z \ket{\psi}\) e \((z+w)\ket{\psi} = z\ket{\psi} + w \ket{\psi}\), por exemplo.
Espaço de estados de 1 qubit
O conjunto
é um espaço vetorial com soma e produto por escalar dados por
Esse espaço vetorial será largamente utilizado nos capítulos seguintes e descreve o espaço de estados de 1 qubit, o análogo do bit clássico.
Base e Dimensão#
Uma base para o espaço vetorial \(\mathbb{C}^n\) é um conjunto de vetores linearmente independentes (LI) e que geram o espaço. Demonstra-se que todas as bases de um espaço vetorial têm o mesmo número de elementos, e define-se a dimensão do espaço vetorial pelo número de elementos de uma base.
O espaço vetorial \(\mathbb{C}^n\) tem dimensão \(n\), isto é, todas as suas bases têm \(n\) vetores. Uma base muito útil é a chamada base computacional, ou base canônica`(O adjetivo “canônico”, na Matemática, tem um sentido de “padrão”, como na expressão “configuração padrão”):
Na base computacional, um vetor \(\ket{\psi} = (z_0 , z_{1} , \ldots , z_{n-1} )\) é escrito como
Numa base qualquer \(\beta = \big\{\ket{b_0}, \ldots, \ket{b_{n-1}} \big\}\), qualquer vetor \(\psi\) pode ser escrito como combinação linear dos vetores dessa base. Os coeficientes da combinação linear, colocados em um vetor coluna, representam o vetor \(\psi\) escrito na base \(\beta\), conforme o esquema abaixo:
O subscrito \(\beta\) pode ser omitido se não houver risco de confusão. Normalmente omite-se esse subscrito quando se trata da base computacional.
Bases para 1 qubit
Há especial interesse no espaço \(\mathbb{C}^2\). Este espaço modela um qubit — o análogo quântico do bit — a ser discutido em mais detalhes posteriormente. O espaço \(\mathbb{C}^2\) tem dimensão \(2\) e admite, entre outras, as seguintes bases:
Essa notação para as bases será justificada a posteriori.
\(\mathcal{X}\) é base para 1 qubit
Para mostrar que
é base do espaço de estados de 1 qubit, deve-se mostrar que os vetores são LI (Linearmente Independentes) e geram o espaço \(\mathbb{C}^2\).
\(\mathcal{X}\) é LI: Considere a combinação linear nula:
Tem-se que
Portanto os coeficientes da combinação linear nula devem ser todos nulos, e isso significa que os vetores \(\ket{+}\) e \(\ket{-}\) são LI.
\(\mathcal{X}\) gera o espaço: Seja \(\ket{\psi} = z_0 \ket{0} + z_1 \ket{1}\) um vetor qualquer de \(\mathbb{C}^2\). Tenta-se escrever \(\ket{\psi}\) como combinação linear de \(\ket{+}\) e \(\ket{-}\). Se for possível, esses vetores geram o espaço.
Assim,
Dessa forma, \(\mathcal{X}\) gera o espaço \(\mathbb{C}^2\) e é base desse espaço.
Comentário: Quando se sabe previamente que a dimensão do espaço é \(n\) e se a lista de vetores candidatos a base tem \(n\) elementos, então as condições de ser LI e gerar o espaço são equivalentes. Em consequência, basta verificar uma das condições para mostrar que os vetores formam uma base. Por exemplo, se sabemos que a dimensão de \(\mathbb{C}^2\) é \(\dim \mathbb{C}^2 = 2\), e temos que \(\mathcal{X}\) tem dois elementos, então bastaria verificar uma das duas condições: \(\mathcal{X}\) é LI ou \(\mathcal{X}\) gera o espaço.
Exercício
Um Qubit se encontra em um estado:
Escreva esse estado utilizando-se da notação de colunas
Exercício
Escreva uma função em Python que recebe uma matriz coluna dado por uma lista ou tuple e retorna ao usuário o a combinação linear dos vetores na notação de Dirac.
Matriz de Mudança de base#
Por vezes é conveniente expressar um vetor em outra base que não a base computacional. Essa mudança de base pode trazer novo insight em algumas situações, bem como tornar os cálculos mais simples e factíveis.
A matriz de mudança de base de \(\beta_{\text{old}} = \big\{\ket{u_0}, \ldots, \ket{u_{n-1}} \big\}\) para \(\beta_{\text{new}} = \big\{ \ket{v_0}, \ldots, \ket{v_{n-1}} \big\}\) é dada por
Isto é, para montar a matriz de mudança de base, os vetores da base nova devem ser escritos como combinação linear dos vetores da base antiga, obtendo vetores coluna. Esses vetores serão as colunas da matriz de mudança de base. Dessa forma, tem-se
A matriz de mudança de base admite matriz inversa, que corresponde à mudança de base da base nova de volta para a base antiga:
Nota
O símbolo \(I\) na matriz de mudança de base \([I]^{\beta_{\text{old}}}_{\beta_{\text{new}}}\) refere-se ao operador identidade. A matriz de mudança de base corresponde à matriz do operador identidade nas bases \(\beta_{\text{old}}\) e \(\beta_{\text{new}}\). As matrizes referente a operadores lineares serão vistas na seção Matriz de uma Transformação Linear.
Exemplo
Considere as bases \(\mathcal{I}\) e \(\mathcal{X}\) apresentadas no exemplo [Base para 1 qubit]. A matriz de mudança de base da base computacional \(\mathcal{I}\) para a base \(\mathcal{X}\) é obtida escrevendo os vetores da base nova (\(\mathcal{X}\)) como combinação linear dos vetores na base antiga (\(\mathcal{I}\)):
Colocam-se as os vetores coluna na ordem em que aparecem na lista:
Essa matriz é conhecida em Computação Quântica como matriz de Hadamard, e costuma ser denotada por \(H\). Portanto
Também vale que a matriz de mudança de base de \(\mathcal{X}\) para \(\mathcal{I}\) é \(H\), visto que
Então:
Produto Interno, Norma e Produto Exterior#
Produto Interno#
O espaço vetorial \(\mathbb{C}^n\) admite o seguinte produto interno:
para \(\ket{\phi} = \begin{bmatrix}w_0 \\ \vdots \\ w_{n-1}\end{bmatrix}\) e \(\ket{\psi} = \begin{bmatrix}z_0 \\ \vdots \\ z_{n-1}\end{bmatrix}\). Pode-se considerar o símbolo \(\bra{\phi}\) de maneira independente, definindo-o como:
em que o símbolo \(\dagger\) denota transposição e conjugação do vetor. Essa notação também será justificada posteriormente.
A operação definida acima satisfaz as propriedades que definem um produto interno de maneira geral:
(PI1) Linearidade no segundo argumento:
\[\big( \ket{\phi} , z_1\ket{\psi_1} + z_2 \ket{\psi_2} \big) = z_1 \big( \ket{\phi} , \ket{\psi_1} \big) + z_2 \big( \ket{\phi} , \ket{\psi_2} \big)\](PI2) Antilinearidade no primeiro argumento:
\[\big( z_1 \ket{\phi_1} + z_2 \ket{\phi_2} , \ket{\psi} \big) = z_1^{\ *} \big( \ket{\phi_1} , \ket{\psi} \big) + z_2^{\ *} \big( \ket{\phi_2} , \ket{\psi} \big)\](PI3) Simetria hermitiana:
\[\big( \ket{\phi} , \ket{\psi} \big)^* = \big( \ket{\psi} , \ket{\phi} \big)\](PI4) Positividade:
\[\big( \ket{\phi} , \ket{\phi} \big) \geq 0 \ \ \ \text{e} \ \ \ \big( \ket{\phi} , \ket{\phi} \big) = 0 \Leftrightarrow \ket{\psi} = 0\]
A propriedade (PI2) decorre de (PI1) e de (PI3), mas foi incluída na lista por completeza. Por causa das propriedades (PI1) e (PI2), o produto interno é dito ser sesquilinear (O prefixo sesqui significa “um e meio”).
O espaço vetorial \(\mathbb{C}^n\) é, pois, dito ser um espaço vetorial com produto interno, ou ainda, um espaço de Hilbert.
Dica
Um espaço de Hilbert é definido como sendo um espaço vetorial com produto interno e com uma propriedade adicional chamada completude. Essa propriedade é automática para espaços de dimensão finita.
Exemplo
O produto interno dos vetores
é dado por:
Esse produto interno também pode ser calculado de maneira matricial:
Exercício
Considere:
(a) Encontre \(\bra{a}\ket{b}\)
(b) Encontre \(\bra{b}\ket{a}\)
(c) Qual a relação entre os resultados obtidos?
Exercício
Escreva uma função em Python que receba dois vetores dados por uma lista ou tuple e retorne o produto interno entre eles na notação de matriz coluna e na notação de Dirac
Norma#
A norma, ou tamanho, de um vetor é definida por
operação bem definida pois \(\braket{\psi}\) é real e não-negativo. Por consequência da propriedade (P4), tem-se \(||{\ket{\psi}}|| = 0 \Leftrightarrow \ket{\psi} = 0\). Um vetor normalizado é um vetor de tamanho unitário, e a operação de normalização consiste em multiplicar o vetor \(\ket{\psi}\) por \(\frac{1}{||{\ket{\psi}}||}\) para que o vetor resultante \(\frac{\ket{\psi}}{||{\ket{\psi}}||}\) tenha norma 1.
Exemplo
Os vetores \(\ket{0}\), \(\ket{1}\), \(\ket{+}\) e \(\ket{-}\) têm norma 1.
Exemplo
A norma do vetor \(\ket{\psi} = \frac{i}{2} \ket{0} + \frac{\sqrt{3}}{2} \ket{1}\) é
Ortogonalidade#
De forma análoga com o que se passa com vetores no \(\mathbb{R}^3\), dois vetores \(\ket{\phi}\) e \(\ket{\psi}\) são ditos ortogonais se o produto interno entre eles é nulo. Em símbolos, \(\ket{\phi} \perp \ket{\psi} \ \Leftrightarrow \ \braket{\phi | \psi} = 0\).
Exemplo
Os vetores \(\ket{0}\) e \(\ket{1}\) são ortogonais:
Exemplo
Os vetores \(\ket{+} = \frac{1}{\sqrt{2}} \ket{0} + \frac{1}{\sqrt{2}} \ket{1}\) e \(\ket{-} = \frac{1}{\sqrt{2}} \ket{0} - \frac{1}{\sqrt{2}} \ket{1}\) são ortogonais:
Base Ortonormal#
Uma base em que todos os vetores são ortogonais dois a dois e têm tamanho 1 é dita ser base ortonormal. Se \(\beta = \{\ket{b_0}, \ldots, \ket{b_{n-1}} \}\) é uma tal base, vale a chamada relação de ortogonalidade
em que \(\delta_{k,l}\) é conhecido como delta de Kronecker, e vale 1 se e somente se os seus dois índices são iguais; se forem diferentes, vale 0.
Um vetor \(\ket{\psi}\) pode ser escrito como combinação linear dos vetores da base \(\beta\) por \(\ket{\psi} = \sum_k a_k \ket{b_k}\). Os coeficientes \(a_k\) podem ser encontrados de maneira simples quando a base é ortonormal. Aplicando-se o produto interno em ambos os lados, tem-se
Percebe-se que isso é análogo à decomposição de um vetor \(\vec{v} \in \mathbb{R}^3\) nas suas componentes \(x\), \(y\) e \(z\) na base canônica. Nesse caso, as componentes do vetor são dadas por \(v_x = \hat{x} \cdot \vec{v}\), \(v_y = \hat{y} \cdot \vec{v}\) e \(v_z = \hat{z} \cdot \vec{v}\), em que \(\cdot\) denota o produto interno no \(\mathbb{R}^3\).
Portanto, os coeficientes do vetor \(\ket{\psi}\) na base ortonormal são obtidos realizando-se projeções de \(\ket{\psi}\) na direção dos vetores unitários \(\ket{b_l}\) da base ortonormal. Assim:
Exemplo
A base \(\ket{0}\), \(\ket{1}\) é ortonormal, em consequência dos exemplos Normal 1 e Ortogonalidade da Base Computacional. As projeções de um vetor \(\ket{\psi} = a_0 \ket{0} + a_1 \ket{1}\) na base computacional são dadas por
e o vetor \(\ket{\psi}\) pode ser escrito como
Exemplo
A base \(\ket{+}\), \(\ket{-}\) é ortonormal em consequência dos exemplos Norma 1 e Ortogonalidade da Base X. Os coeficientes do vetor \(\ket{\psi} = \frac{1}{2} \left( \ket{0} + i \sqrt{3} \ket{1} \right)\) na base \(\mathcal{X}\) são dados por:
Portanto,
Desigualdade de Cauchy-Schwarz#
Há uma desigualdade envolvendo normas de vetores que é válida de maneira geral, para quaisquer espaços vetoriais equipados com produto interno e norma. É conhecida por desigualdade de Cauchy-Schwarz.
Desigualdade de Cauchy-Schwarz
Dados \(\ket{u}, \ket{v} \in V\), com \(V\) um espaço vetorial qualquer munido de produto interno e norma, vale que
A igualdade ocorre se e somente se os vetores \(\ket{u}\) e \(\ket{v}\) forem múltiplos um do outro.
Demonstração. Considere o vetor \(a\ket{u} - b\ket{v}\). O produto interno desse vetor consigo mesmo deve ser real e não-negativo, por propriedade do produto interno, portanto
Escolhendo \(a = \braket{v | v}\) e \(b = \braket{v | u}\), tem-se
Logo, obtém-se
e fica provada a desigualdade.
Ocorre igualdade se e somente se ocorrer igualdade em \(0 \leq \big( a^{*}\bra{u} - b^{*}\bra{v} \big) \big(a \ket{u} - b \ket{v} \big)\), isto é, se e somente se o vetor \(a \ket{u} - b \ket{v}\) for nulofootnote{Isso é devido à propriedade (PI4) do produto interno.}. Portanto deve-se ter um dos vetores \(\ket{u}\), \(\ket{v}\) múltiplo do outro.
No espaço vetorial \(\mathbb{R}^n\) essa desigualdade permite definir o conceito de ângulo entre dois vetores por meio da relação \(\cos \theta = \frac{\overrightarrow{u} \cdot \overrightarrow{v}}{||{\overrightarrow{u}||} ||{\overrightarrow{v}}}||\). No caso de interesse para o presente trabalho, o do espaço vetorial \(\mathbb{C}^n\), essa interpretação não é possível pois o produto interno pode assumir um valor complexo.
Matriz de Mudança de Base entre Bases Ortonormais#
Da mesma forma que em Matriz de Mudança de Base, é possível escrever uma matriz que faz a mudança de base entre duas bases ortonormais \(\beta_{\text{old}} = \big\{\ket{u_0}, \ldots, \ket{u_{n-1}} \big\}\) e \(\beta_{\text{new}} = \big\{ \ket{v_0}, \ldots, \ket{v_{n-1}} \big\}\). As colunas da matriz de mudança de base são os vetores da base nova escritos como combinação linear dos vetores da base antiga. Como as bases são ortonormais, esses coeficientes podem ser obtidos pela projeção na direção dos vetores da base, como descrito na seção Base Ortonormal.
A matriz de mudança de base, nesse caso, é dada por
A matriz de mudança de base satisfaz \([I]^{\beta_{\text{old}}}_{\beta_{\text{new}} }\phantom{\big{|}}^{-1} = [I]^{\beta_{\text{old}}}_{\beta_{\text{new}} }\phantom{\big{|}}^{\dagger} = [I]^{\beta_{\text{new}}}_{\beta_{\text{old}} }\).
Isso significa que a matriz de mudança de base é unitária, um assunto que será visto na seção Operadores Unitários.
Exemplo
Sabendo que as bases \(\mathcal{I}\) e \(\mathcal{X}\) são ortonormais, pode-se encontrar a matriz de mudança de base fazendo as seguintes contas.
Portanto, a matriz de mudança de base de \(\mathcal{I}\) para \(\mathcal{X}\) é dada por:
Esse é o mesmo resultado obtido no exemplo Matrix Mudança de Base.
Produto Exterior#
É possível dar um significado ao símbolo \(\bra{\phi}\) como sendo um vetor linha. Isso permite, pois, considerar-se o produto matricial \(\ket{\psi} \cdot \bra{\phi} = \ket{\psi}\bra{\phi}\) de um vetor linha \(n\times 1\) por um vetor coluna \(1 \times n\), resultando em uma matriz \(n \times n\). Essa operação é chamada de produto exterior.
Exemplo
No espaço vetorial de 1 qubit, alguns exemplos de produto exterior são:
Transformações Lineares#
Transformação Linear e Operador Linear#
Uma transformação linear é uma aplicação \(T \colon \mathbb{C}^n \to \mathbb{C}^m\) que respeita a soma e a multiplicação por escalar, ou seja, tal que valem:
(TL1) Preservação da soma:
\[T(\ket{\phi} + \ket{\psi}) = T\ket{\phi} + T\ket{\psi}\](TL2) Preservação do produto por escalar:
\[T( z\ket{\psi} ) = z \cdot T\ket{\psi} \ .\]
Um operador linear é uma transformação linear \(A \colon \mathbb{C}^n \to \mathbb{C}^n\) (\(m=n\)).
Exemplo
A função \(H \colon \mathbb{C}^2 \to \mathbb{C}^2\) dada por
é uma transformação linear. De fato, as propriedades de transformação linear se verificam para \(H\).
Preservação da soma: Sejam \(\ket{\phi} = a_0 \ket{0} + a_1 \ket{1}\) e \(\ket{\psi} = b_0 \ket{0} + b_1 \ket{1}\).
\[\begin{split}\begin{eqnarray*} H(\ket{\phi} + \ket{\psi}) &=& H \left( a_0 \ket{0} + a_1 \ket{1} + b_0 \ket{0} + b_1 \ket{1} \right) \\ &=& H\left( (a_0 + b_0) \ket{0} + (a_1 + b_1) \ket{1} \right) \\ &=& \frac{(a_0 + b_0) + (a_1 + b_1)}{\sqrt{2}} \ket{0} + \frac{(a_0 + b_0) - (a_1 + b_1)}{\sqrt{2}} \\ &=& \frac{a_0 + a_1}{\sqrt{2}} \ket{0} + \frac{a_0-a_1}{\sqrt{2}} + \frac{b_0 + b_1}{\sqrt{2}} \ket{0} + \frac{b_0-b_1}{\sqrt{2}} \\ &=& H \ket{\phi} + H \ket{\psi} \end{eqnarray*}\end{split}\]Preservação do produto por escalar: Sejam \(z \in \mathbb{C}\) e \(\ket{\psi} = a_0 \ket{0} + a_1 \ket{1}\).
\[\begin{split}\begin{eqnarray*} H(z \ket{\psi}) &=& H \big( z(a_0 \ket{0} + a_1 \ket{1}) \big) \\ &=& H \left( za_0 \ket{0} + za_1 \ket{1}) \right) \\ &=& \frac{za_0 + za_1}{\sqrt{2}} \ket{0} + \frac{za_0-za_1}{\sqrt{2}} \\ &=& z \left( \frac{a_0 + a_1}{\sqrt{2}} \ket{0} + \frac{a_0-a_1}{\sqrt{2}} \right) \\ &=& z\cdot H \ket{\psi} \end{eqnarray*}\end{split}\]
Funcional Linear#
Um funcional linear é uma transformação linear \(f \colon \mathbb{C}^n \to \mathbb{C}\) (\(m=1\)). O bra \(\bra{\phi}\) pode ser pensado como um funcional linear que pode atuar em um vetor coluna \(\ket{\psi}\) para resultar no número complexo \(\braket{\phi | \psi}\). Pode-se verificar que todo funcional linear é da forma \(\bra{\phi} = \braket{\phi | \cdot}\) para algum \(\ket{\phi}\).
Exemplo
O bra \(\bra{0}\) é um funcional linear que leva \(\ket{\psi}\) no coeficiente \(\braket{0 | \psi}\) da projeção na direção \(\ket{0}\). Igualmente, o bra \(\bra{1}\) é um funcional linear que leva \(\ket{\psi}\) no coeficiente \(\braket{1 | \psi}\) da projeção na direção \(\ket{1}\).
Projeção e Relação de Completude#
Se \(\ket{u}\) for unitário, o funcional linear \(\bra{u}\) leva um ket \(\ket{\psi}\) em \(\braket{u | \psi}\), que corresponde ao coeficiente da projeção de \(\ket{\psi}\) na direção de \(\ket{u}\).
O vetor \(\braket{u | \psi}\ket{u}\) é a projeção de \(\ket{\psi}\) na direção do vetor unitário \(\ket{u}\). Movendo-se o número \(\braket{u | \psi}\) para a direita, pode-se escrever essa projeção como \(\text{proj}_{\ket{u}} \ket{\psi} = \ket{u}\bra{u}\ket{\psi}\). O operador \(\ket{u}\bra{u}\) é, então, chamado operador projeção na direção de \(\ket{u}\)
Se \(\beta = \{\ket{b_0}, \ldots, \ket{b_{n-1}} \}\) é uma base ortonormal, pode-se escrever qualquer vetor \(\ket{\psi}\) como soma das suas projeções ortogonais sobre as direções definidas pelos vetores da base. Dessa forma, tem-se
Segue que
expressão conhecida como relação de completude.
Exemplo
A projeção ortogonal da direção do vetor \(\ket{0}\) é o operador \(\ket{0}\bra{0}\), visto que sua ação em um ket \(\ket{\psi}\) é dada por \(\ket{0}\bra{0} \ket{\psi} = \braket{0 | \psi} \ket{0}\) e a projeção ortogonal na direção de \(\ket{1}\) é o operador de projeção \(\ket{1}\bra{1}\), pois \(\ket{1}\bra{1} \ket{\psi} = \braket{1 | \psi} \ket{1}\).
A relação de completude no espaço vetorial dos estados de 1 qubit, \(\mathbb{C}^2\), é dada por
Definição de uma Transformação Linear nos Elementos da Base#
Para definir uma transformação linear, basta que se forneça como ela atua nos elementos de uma base. Isto é, dada \(\beta = \{\ket{b_0}, \ldots, \ket{b_{n-1}} \}\) base de \(\mathbb{C}^n\), pode-se obter \(T\ket{\psi}\) conhecendo-se \(T\ket{b_k}\) para todo \(k\). De fato, como \(\beta\) base, pode-se escrever \(\ket{\psi}\) como combinação linear
Aplicando-se a transformação \(T\) e usando a linearidade, obtém-se
e dessa forma, \(T\ket{\psi}\) pode ser obtido a partir dos \(T\ket{b_k}\)’s.
Exemplo
Considere o operador linear em 1 qubit \(X \colon \mathbb{C}^2 \to \mathbb{C}^2\) definido nos vetores da base computacional por
O operador \(X\) está bem definido em todo \(\ket{\psi} = a \ket{0} + b \ket{1}\) graças à sua linearidade:
Matriz de uma Transformação Linear#
Seja \(T \colon U= \mathbb{C}^n \to V=\mathbb{C}^m\) uma transformação linear. Sejam \(\beta_U = \{\ket{u_0}, \ldots, \ket{u_{n-1}} \}\) base de \(U\) e \(\beta_V = \{ \ket{v_0} , \ldots , \ket{v_{n-1}} \}\) base de \(V\). Quando fixadas bases para os espaços vetoriais do domínio e do contradomínio de \(T\), é possível representar a transformação \(T\) por uma matriz, de forma que a atuação de \(T\) sobre um vetor \(\ket{\psi}\) é equivalente ao produto matriz-vetor coluna.
A matriz da transformação linear \(T\) nas bases \(\beta_U\) e \(\beta_V\) é dada por:
Definida dessa forma, vale que:
portanto, a atuação da matriz de \(T\) sobre um ket é equivalente à multiplicação matriz-vetor coluna levando-se em consideração as bases previamente fixadas.
Considere que as bases \(\beta_U\) e \(\beta_V\) sejam ortonormais. Cada vetor \(T\ket{u_k}\) pode ser escrito na base \(\beta_V\) da seguinte forma:
tendo em vista que a \(l\)-ésima entrada do vetor é o coeficiente da projeção de \(\ket{Tu_k}\) na direção do \(l\)-ésimo vetor da base em \(V\). Assim, a entrada de linha \(l\) e coluna \(k\) da matriz \([T]^{\beta_U}_{\beta_V}\) é \(\braket{v_l | Tu_k}\), com \(l = 0, \ldots , m-1\) e \(k=0, \ldots , n-1\) e consequentemente
No caso de um operador linear, tem-se \(U=V\) (\(m=n\)), e é possível escolher a mesma base \(\beta = \{\ket{b_0}, \ldots, \ket{b_{n-1}} \}\) para o domínio e o contradomínio da transformação. Essa é uma situação bastante frequente, e a matriz associada ao operador linear é montada da seguinte forma: as colunas da matriz são os vetores \(\ket{Tb_k}\) escritos como vetores coluna na base \(\beta\). Portanto:
Se a base \(\beta\) for ortonormal, obtém-se que
Exemplo
Um operador linear \(A\) sobre um qubit pode ser escrito como uma matriz (na base computacional) \(2\times2\) com coeficientes complexos da seguinte forma:
com \([\cdot]\) significando que os vetores em questão estão escritos como vetores coluna na base computacional. É frequente denotar a matriz do operador \(A\) pelo mesmo símbolo \(A\), quando está implícito qual base é considerada.
Exemplo
A matriz da transformação linear do exemplo Transformação Linear nos Elementos da Base, na base computacional, é obtida escrevendo-se a ação de \(X\) sobre os vetores da base.
Em seguida, monta-se a matriz fazendo
Matrizes de Pauli
As matrizes
são conhecidas como matrizes de Pauli. Essas são representações na base computacional dos operadores \(X\), \(Y\) e \(Z\). Usa-se, costumeiramente, a mesma notação para se referir ao operador e à sua matriz na base computacional.
Em determinadas situações, a matriz identidade \(I\) também é chamada matriz de Pauli, e usa-se a notação alternativa
Matriz da Composição de Transformações Lineares#
A composição de transformações lineares \(T \colon U \to V\) e \(R \colon V \to W\) é a transformação linear denotada por \(R T = R \circ T \colon U \to W\) e tal que \(RT(\ket{\psi}) = R \Big( T\big(\ket{\psi}\big) \Big)\) para todo \(\ket{\psi}\). A matriz dessa transformação linear pode ser obtida pela multiplicação matricial das matrizes de \(R\) e de \(T\):
em que \(\beta_U\), \(\beta_V\) e \(\beta_W\) são bases de \(U\), \(V\) e \(W\), respectivamente.
Mudança de Base#
Para escrever a matriz de uma transformação linear \(T\colon U \to V\) em novas bases \(\beta_U^\prime\) e \(\beta_V^\prime\) basta aplicar matrizes de mudança de base de maneira apropriada.
No caso de um operador linear \(A \colon V \to V\), pode-se usar a mesma base nos espaços vetoriais do domínio e do contradomínio da função. A mudança de base nesse caso fica:
A transformação matricial \([A] \to [A]^\prime = [M]^{-1} [A] [M]\) é conhecida como transformação de similaridade. Duas transformações conectadas dessa forma são ditas matrizes semelhantes. As matrizes semelhantes são representantes de um mesmo operador linear escrito em bases diferentes.
Se as bases \(\beta_U\) e \(\beta_U^\prime\) forem ortonormais, a fórmula para mudança de base fica:
em que a operação simbolizada por \(\dagger\) é a transposição e conjugação da matriz. Essa operação será introduzida formalmente na seção Operador Adjunto.
Matrizes de Pauli
Considere as bases \(\mathcal{I}\) e \(\mathcal{X}\) apresentadas no exemplo [Base para 1 qubit]. A matriz de mudança de base de \(\mathcal{I}\) para \(\mathcal{X}\) e vice-versa é a matriz de Hadamard \(H\), como visto no exemplo Matrix Mudança de Base. O operador \(X\), visto no exemplo Matrizes de Pauli, cuja matriz na base computacional é
pode ser representado na base \(\mathcal{X}\) por
Autovalores, Autovetores e Decomposição Espectral#
Autovalores e Autovetores#
Seja \(A\) um operador linear, com matriz na base computacional também representada por \(A\). Os autovalores de \(A\) são os números complexos \(\lambda\) que satisfazem
Os vetores não nulos \(\ket{v}\) que satisfazem a equação acima são chamados autovetores de \(A\) associados ao autovalor \(\lambda\).
Exemplo
O operador linear em 1 qubit \(Z\) definido pela matriz
possui:
autovalor \(1\), pois o vetor não nulo \(\ket{0}\) é tal que \(Z \ket{0} = 1 \cdot \ket{0}\);
autovalor \(-1\), pois o vetor não nulo \(\ket{1}\) satisfaz \(Z \ket{1} = -1 \cdot \ket{1}\).
Cálculo de Autovalores#
A equação de autovalores \(A \ket{v} = \lambda \ket{v}\) é equivalente a \(\big(A-\lambda I \big) \ket{v} = 0\), com \(\ket{v} \neq 0\), e isso é equivalente a dizer que a matriz de \(A-\lambda I\) é singular. Por sua vez, isso equivale à equação
Com a equação acima, consegue-se encontrar os autovalores \(\lambda\) do operador \(A\) encontrando-se as raízes do polinômio característico \((A-\lambda I)\). Esse polinômio têm grau \(n\) e, como estamos buscando raízes nos números complexos, admite \(n\) raízes (pode acontecer que sejam repetidas). Dessa forma, todo operador admite um autovalor (isso não é necessariamente válido para espaços vetoriais reais).
Exemplo
Os autovalores da matriz
podem ser obtidos por:
Os autovalores podem ser números complexos. Como a matriz é \(2\times2\), foi obtido um polinômio característico de grau 2 e foram obtidas 2 raízes.
Cálculo de Autovetores#
Uma vez descobertos os autovalores \(\lambda\), retorna-se à equação \(A \ket{v} = \lambda \ket{v}\), ou melhor, à equação
para encontrar todos os autovetores \(\ket{v} \neq 0\) satisfazendo essa equação. Como a matriz \(A-\lambda I\) é singular (essa é a condição para se encontrar \(\lambda\)), a equação em questão admite infinitas soluções \(\ket{v}\), formando um sistema linear possível e indeterminado.
Em algumas situações é possível montar uma base para o espaço composta por autovetores do operador \(A\). Há condições sobre o operador que revelam se é possível obter uma base ortonormal de autovetores. Isso será visto na seção Tipos Especiais de Operadores. A obtenção de uma base de autovetores permite escrever a matriz \(A\) nessa base como uma matriz diagonal, o que se prova útil em diversas circunstâncias.
Exemplo
Dada a matriz
os autovalores e autovetores são encontrados a seguir.
Autovalores: Resolvendo \(\det(X - \lambda I) = 0\), obtém-se:
\[\begin{split}\begin{eqnarray*} & & \det(X - \lambda I) = 0 \\ & & \det \begin{bmatrix} -\lambda & 1 \\ 1 & -\lambda \end{bmatrix} = 0 \\ & & \lambda^2 - 1 = 0 \\ & & \lambda = \pm 1 \ . \end{eqnarray*}\end{split}\]Autovetores: Para cada autovalor \(\lambda\), deve-se resolver
\[\big(X-\lambda I \big) \ket{v} = 0 \ ,\]obtendo-se o vetor \(\ket{v}\).
Para \(\lambda = -1\):
\[\begin{split}\begin{eqnarray*} \big(X-\lambda I \big) \ket{v} &=& 0 \\ \begin{bmatrix} -1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} a_0 \\ a_1\end{bmatrix} &=& \begin{bmatrix} 0 \\ 0 \end{bmatrix} \end{eqnarray*}\end{split}\]\[\begin{split}\begin{cases} -a_0 + a_1 = 0 \\ \phantom{-}a_0 - a_1 = 0 \end{cases}\end{split}\]O sistema resultante, como esperado, é possível e indeterminado. Resolvendo o sistema, tem-se:
\[\begin{split}\begin{cases} a_0 = a_1 \\ a_1 \in \mathbb{C} \ . \end{cases}\end{split}\]Os autovetores associados ao autovalor \(\lambda = -1\) são:
\[\begin{split}\ket{v} = \begin{bmatrix} a_1 \\ a_1 \end{bmatrix} = a_1 \begin{bmatrix} 1 \\ 1 \end{bmatrix} \ \ \text{ com } a_1 \in \mathbb{C}, a_1 \neq 0\end{split}\]O autoespaço associado a \(\lambda = -1\) é o subespaço vetorial:
\[\begin{split}V_{-1} = \left\lbrace a_1 \begin{bmatrix} 1 \\ 1 \end{bmatrix} \colon a_1 \in \mathbb{C} \right\rbrace \ = \text{span}\left\lbrace \begin{bmatrix} 1 \\ 1 \end{bmatrix} \right\rbrace .\end{split}\]
Para \(\lambda = 1\):
O sistema é possível e indeterminado, e, resolvendo o sistema, tem-se:
Os autovetores associados ao autovalor \(\lambda = 1\) são:
O autoespaço associado a \(\lambda = 1\) é o subespaço vetorial:
Diagonalização de Operadores#
Uma vez encontrados os autovalores \(\lambda_j\) e uma base de autovetores \(\mathcal{V} = \{ \ket{v_j} , j=0, \ldots , n-1 \}\), com \(\ket{v_j}\) associado ao autovalor \(\lambda_j\), o operador linear \(A\) pode ser escrito na base \(\mathcal{V}\) como uma matriz diagonal. Defina as matrizes:
A matriz de \(A\) na base \(\mathcal{V}\) é dada por:
A matriz \(M\) nada mais é que a matriz de mudança de base \(M=[I]^{\mathcal{I}}_{\mathcal{V}}\). Conforme a seção Matriz de Mudança de Base , pode-se escrever:
Ainda, se a base \(\mathcal{V}\) for ortonormal, conforme Base Ortonormal, pode-se escrever
Nessas expressões, usa-se \(A\) para denotar a matriz \([A]\) do operador \(A\) na base computacional, o que simplifica a notação quando não houver risco de confusão.
Portanto, de posse dos autovalores e de uma base ortonormal, é possível escrever o operador \(A\) como uma matriz diagonal.
O operador \(A\) também pode ser representado na notação do produto exterior da seguinte forma. Como \(\mathcal{V}\) forma uma base ortonormal, vale a relação de completude \(I = \sum_k \ket{v_k}\bra{v_k}\) para essa base. Aplicando-se essa relação a \(A\), obtém-se
Exemplo
No exemplo Autovetores X foram calculados os autovalores e autovetores da matriz
obtendo-se:
\(\lambda = 1\phantom{-}\) , \(\ket{v} = a \begin{bmatrix} 1 \\ 1 \end{bmatrix}\) \(\phantom{-}\) \((`a \in \mathbb{C}, a \neq 0\))$
\(\lambda = -1\) , \(\ket{v} = a \begin{bmatrix}\phantom{-}1 \\ -1 \end{bmatrix}\) (\(a \in \mathbb{C}, a \neq 0\))
Pretende-se extrair uma base ortonormal de autovetores para escrever \(X\) na forma diagonal. Nesse caso (Todos os autoespaços de dimensão 1.), basta normalizar os autovetores obtidos.
Para \(\lambda = -1\):
\[\begin{split}||{a \begin{bmatrix} 1 \\ 1 \end{bmatrix} }|| = 1 \implies |{a}| \sqrt{1^2 + 1^2} = 1 \implies |{a}| = \frac{1}{\sqrt{2}} \ .\end{split}\]Há várias opções para \(a\) que satisfazem essa condição. Pode-se escolher apenas uma delas para fazer a diagonalização, por exemplo: \(a = \frac{1}{\sqrt{2}}\). O autovetor normalizado é, portanto,
\[\begin{split}\ket{v} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \frac{1}{\sqrt{2}} \ket{0} + \frac{1}{\sqrt{2}} \ket{1} \ .\end{split}\]Para \(\lambda = 1\):
\[\begin{split}||{a \begin{bmatrix} \phantom{-}1 \\ -1 \end{bmatrix} }|| = 1 \implies |{a}| \sqrt{1^2 + (-1)^2} = 1 \implies |{a}| = \frac{1}{\sqrt{2}} \ .\end{split}\]Do mesmo modo, pode-se escolher \(a = \frac{1}{\sqrt{2}}\), e o autovetor normalizado é:
\[\begin{split}\ket{v} = \frac{1}{\sqrt{2}} \begin{bmatrix}\phantom{-} 1 \\ -1 \end{bmatrix} = \frac{1}{\sqrt{2}} \ket{0} - \frac{1}{\sqrt{2}} \ket{1} \ .\end{split}\]Base ortonormal de autovetores:
\[\begin{split}\underbrace{\ket{v_0} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 1 \end{bmatrix}}_{\lambda = 1} \ \ , \ \ \underbrace{\ket{v_1} = \frac{1}{\sqrt{2}} \begin{bmatrix}\phantom{-} 1 \\ -1 \end{bmatrix}}_{\lambda = -1}\end{split}\]Diagonalização da matriz:
Matriz de \(X\) na forma diagonal:
\[\begin{split}X_D = \begin{bmatrix}\lambda_0 & \\ & \lambda_1\end{bmatrix} = \begin{bmatrix}1 & \\ & -1 \end{bmatrix}\end{split}\]Matriz de mudança de base:
\[\begin{split}M = \begin{bmatrix} | & | \\ \ket{v_0} & \ket{v_{1}} \\ | & | \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ & \\ \phantom{-}\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & \phantom{-}1 \\ 1 & -1 \end{bmatrix}\end{split}\]Operador na forma diagonal: Na notação de produto exterior, tem-se:
Tipos Especiais de Operadores#
Nesta seção, alguns operadores com propriedades especiais serão apresentados. Os operadores normais, hermitianos, unitários, positivos e projetivos participam da base da Mecânica Quântica.
Operador Adjunto#
Seja \(A\) um operador linear. Em Álgebra Linear, é possível demonstrar que existe um único operador linear, denotado por \(A^{\dagger}\) e chamado operador adjunto de \(A\), que satisfaz a seguinte propriedade:
(OA1) \(\big( \ket{\phi} , A\ket{\psi} \big) = \big( A^{\dagger}\ket{\phi} , \ket{\psi} \big)\) Para qualquer base \(\beta\), a matriz do operador \(A^{\dagger}\) está relacionada com a matriz de \(A\) por
(OA2) \([A^\dagger ]_\beta = [A]_\beta^{\ \dagger} = \big( [A]_\beta^{\ *}\big)^{T}\) isto é, a matriz \([A]_\beta^{\ \dagger}\) é obtida de \([A]_\beta\) conjugando suas entradas e tomando a transposta.
Algumas propriedades da adjunta estão dispostas na seguinte lista:
\(\big( A^\dagger \big)^\dagger = A\) (Involução)
\(\displaystyle \left( \sum_k a_k A_k \right)^{\dagger} = \sum_k a_k^{\ *} A_k^{\ \dagger}\) (Antilinearidade)
Exemplo
A matriz adjunta de
é a matriz conjugada transposta
Operadores Normais#
Um operador é dito normal se comuta com seu operador adjunto:
(ON) \(A \cdot A^{\dagger} = A^{\dagger} \cdot A\)
Exemplo
O operador definido pela matriz
é normal, pois satisfaz \(A A^\dagger = A^\dagger A\). De fato,
e tem-se que
A importância do operador normal decorre do seguinte teorema:
Teorema Espectral
Um operador é normal se, e somente se, for diagonalizável.
Dessa forma, basta checar se um operador é normal para se saber se ele admite uma base de autovetores e uma representação por matriz diagonal.
Operadores Hermitianos ou Autoadjuntos#
Um operador \(H\) é dito hermitiano, ou autoadjunto se valer a seguinte propriedade:
(OH) \(H^{\dagger} = H\)
Exemplo
O operador dado por
é autoadjunto, pois
Os operadores hermitianos estão relacionados com a evolução no tempo de um sistema quântico fechado e com a medida de um observável.
Um operador hermitiano é, automaticamente, um operador normal, tendo em vista que \(H H^\dagger = H^2 = H^\dagger H\). Conforme o teorema Teorema Espectral: Operador Normal, todo operador hermitiano é, pois, diagonalizável. Além disso, há um teorema que permite tirar conclusões a respeito dos autovalores de uma matriz hermitiana.
Teorema Espectral para Matrizes Hermitianas
Um operador normal é hermitiano se, e somente se, todos os seus autovalores são reais.
Operadores Unitários#
Um operador \(U\) é dito unitário se satisfizer alguma das condições equivalentes:
(OU1) \(U^{\dagger} = U^{-1}\).
(OU2) As linhas ou as colunas de \([U]_\beta\) são vetores ortonormais em \(\mathbb{C}^n\), para alguma base \(\beta\).
(OU3) \(U\) é uma isometria, isto é, preserva o produto interno entre vetores (e em consequência, preserva também a distância entre vetores): \(\big( U\ket{\phi} , U\ket{\psi} \big) = \big( \ket{\phi} , \ket{\psi} \big)\).
Exemplo
O operador definido pela matriz
é unitário, pois as colunas \(\ket{c_0} = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ 1\end{bmatrix}\) e \(\ket{c_1} = \frac{1}{\sqrt{2}} \begin{bmatrix}\phantom{-}1 \\ -1 \end{bmatrix}\) são vetores ortonormais:
O produto de dois operadores unitários é unitário:
A condição de um operador ser unitário também implica normalidade, visto que \(U U^\dagger = I = U^\dagger U\). De acordo com o teorema Teorema Espectral: Operador Normal, todo operador unitário é, então, diagonalizável. Pode-se mostrar o seguinte teorema.
Teorema Espectral para Operadores Unitários
Seja \(U\) uma matriz normal. \(U\) é uma matriz unitária se, e somente se, os seus autovalores são números complexos de módulo 1, logo exprimíveis na forma \(\lambda = e^{i\theta}\) para algum \(\theta \in \mathbb{R}\).
Operadores Positivos#
Um operador é dito positivo quando satisfaz a seguinte propriedade:
(OPos) \(\bra{\psi}P\ket{\psi} \geq 0 \ , \ \ \forall \ket{\psi}\).
É possível demonstrar que um operador positivo é, automaticamente, hermitiano, e, portanto, todos os seus autovalores são reais. Além disso, a propriedade (OPos) é equivalente a dizer que todos os autovetores de \(P\) são números reais não-negativos \(\lambda \geq 0\).
Diz-se que um operador é positivo definido quando satisfaz a condição seguinte, mais rigorosas que (OPos):
(OPosDef) \(\bra{\psi}P\ket{\psi} > 0 \ , \ \ \forall \ket{\psi}\neq 0\)
Essa condição é equivalente a afirmar que todos os autovalores de \(P\) são números reais positivos \(\lambda >0\).
Exemplo
O operador definido pela matriz
é positivo. De fato, por se tratar de uma matriz triangular, os autovalores podem ser obtidos diretamente da diagonal: \(\lambda = 1\) e \(\lambda = 2\). Seus autovalores são todos não negativos, do que decorre que \(A\) é positivo. Como nenhum autovalor é nulo, o operador é também positivo definido.
Operadores de Projeção#
Um operador de projeção é um operador \(P\) que satisfaz:
(OProj) \(P^2 = P\).
Os autovalores de \(P\) podem assumir os valores \(\lambda = 0\) ou \(\lambda = 1\). De fato, se \(\lambda\) é um autovalor com autovetor \(\ket{v}\neq 0\) associado, tem-se \(P\ket{v} = \lambda \ket{v} \implies \lambda \ket{v} = P\ket{v} = PP\ket{v} = \lambda P\ket{v} = \lambda^2 \ket{v}\), logo, \((\lambda^2 - \lambda)\ket{v} = 0\) e, como \(\ket{v} \neq 0\), tem-se \(\lambda^2 - \lambda = 0\) e, por fim, \(\lambda = 0\) ou \(\lambda = 1\). Isso prova, em virtude dos teoremas Teorema Espectral: Operador Hermitiano e Teorema Espectral: Operador Unitário, que todo operador de projeção é hermitiano e positivo.
Considere o subspaço vetorial de dimensão finita \(W = P(V)\) (imagem de \(P\)). Seja \(k=\dim W\) e tome uma base ortonormal \(\big\{ \ket{v_0}, \ldots , \ket{v_{k-1}} \big\}\) de \(P(V)\). Estendendo-se a \(\big\{ \ket{v_0}, \ldots , \ket{v_{k-1}}, \ket{v_k} , \ldots , \ket{v_{n-1}} \big\}\) base ortonormal do espaço \(V\), é possível escrever o operador \(P\) como
O operador
é um operador de projeção no subespaço \(W^{\perp}\).
Tem-se que \(\text{Proj}_W + \text{Proj}_{W^\perp} = I\) e portanto, todo vetor \(\ket{\psi}\) pode ser decomposto na soma de projeções em \(W\) e em \(W^{\perp}\):
Exemplo
Os operadores no espaço de estados de 1 qubit
são as projeções na direção dos vetores \(\ket{0}\) e \(\ket{1}\), respectivamente. Tem-se que
que é a relação de completude.
Se denotarmos por \(W = \text{span}\{\ket{0} \}\) o subespaço gerado por \(\ket{0}\), tem-se que \(W^\perp = \text{span}\{ \ket{1} \}\), \(\ket{0}\bra{0} = \text{Proj}_W\), \(\ket{1}\bra{1} = I - \ket{0}\bra{0} = \text{Proj}_{W^\perp}\) e qualquer vetor \(\ket{\psi}\) pode ser escrito como
Se \(\ket{\psi} = a \ket{0} + b \ket{1}\), então
Resumo#
A figura abaixo traz um quadro resumo dos operadores especiais abordados neste capítulo.
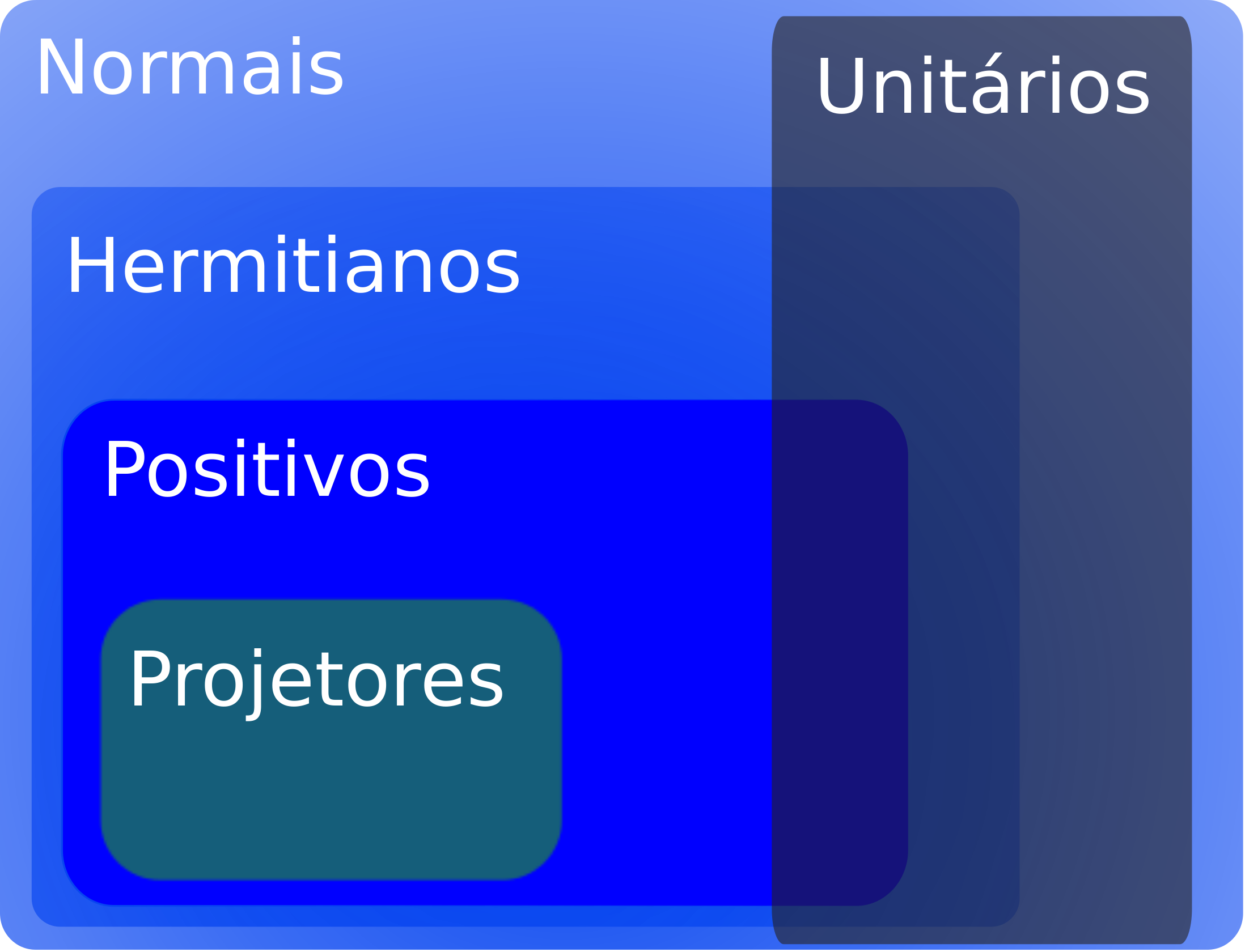
Fig. 1 Relação entre os operadores especiais estudados neste capítulo. Fonte: Slides de Álgebra Linear, UFSM.#
Operador |
Propriedade |
|---|---|
Normal |
\(N N^\dagger = N^\dagger N\) |
Autoadjunto ou Hermitiano |
\(H^\dagger = H\) |
Unitário |
\(U^{-1} = U^\dagger\) |
Projetor |
\(P^2 = P\) |
Positivo |
\(\bra{\psi}P\ket{\psi} \geq 0 \ , \ \ \forall \ket{\psi}\) |
Positivo definido |
\(\bra{\psi}P\ket{\psi} > 0 \ , \ \ \forall \ket{\psi}\neq 0\) |
Produto Tensorial#
É possível compor dois espaços vetoriais para formar um terceiro espaço. Uma maneira de fazer isso é por meio do produto tensorial. Em Computação Quântica, essa construção é fundamental para se trabalhar com sistemas compostos por mais de um qubit. Um sistema de dois qubits será o produto tensorial de dois espaços \(\mathbb{C}^2\), que modelam um qubit.
Espaço Vetorial do Produto Tensorial#
Dados dois espaços vetorias \(V\) e \(W\), com bases \(\beta_V = \{ \ket{v_k} \}\) e \(\beta_W = \{ \ket{w_l} \}\), o produto tensorial de \(V\) e \(W\), denotado por \(V\otimes W\), é definido como o espaço vetorial gerado pela base:
A dimensão do espaço vetorial do produto tensorial é, portanto,
O produto tensorial \(\otimes\) forma uma dupla ordenada com propriedades diferentes das do produto cartesiano. Essas propriedades, listadas abaixos, são chamadas conjuntamente de bilinearidade:
Para todos \(z \in \mathbb{C}\), \(\ket{v}\in V\) e \(\ket{w} \in W\),
\[z \cdot (\ket{v} \otimes \ket{w}) = (z\ket{v}) \otimes \ket{w} = \ket{v} \otimes(z\ket{w}) \ .\]Para todos \(\ket{v^1},\ket{v^2}\in V\) e \(\ket{w} \in W\),
\[(\ket{v^1}+ \ket{v^2}) \otimes \ket{w} = \ket{v^1} \otimes \ket{w} + \ket{v^2} \otimes \ket{w} \ .\]Para todos \(\ket{v}\in V\) e \(\ket{w^1},\ket{w^2} \in W\),
\[\ket{v} \otimes (\ket{w^1} + \ket{w^2}) = \ket{v} \otimes \ket{w^1} + \ket{v} \otimes \ket{w^2} \ .\]
Um elemento genérico do espaço \(V\otimes W\) é uma combinação linear dos vetores da base \(\ket{v_k} \otimes \ket{w_l}\). Em geral, essa combinação não pode ser escrita da forma fatorada \(\ket{v} \otimes \ket{w}\).
Exemplo
O sistema composto por 2 qubits é dado pelo produto tensorial de dois espaços vetoriais de 1 qubit. Esse espaço vetorial é denotado por \(\mathbb{C}^2 \otimes \mathbb{C}^2\). A base desse espaço é formada pelos 4 vetores
e as igualdades apresentadas acima apenas referem-se a notações alternativas e mais compactas. A ordem em que as entradas aparecem no produto tensorial é importante, de forma que \(\ket{01} \neq \ket{10}\), por exemplo.
Um vetor qualquer \(\ket{\psi} \in \mathbb{C}^2 \otimes \mathbb{C}^2\) pode ser escrito como
com \(a,b,c,d \in \mathbb{C}\). Alguns exemplos de vetores pertencentes ao espaço em questão são:
As igualdades acima são exemplos da bilinearidade do produto tensorial.
Comparação do Produto Tensorial com o Produto Cartesiano#
O produto cartesiano, às vezes chamado soma direta é outra maneira de se compor dois espaços vetoriais em um espaço “maior”, denotado por \(V \times W\) ou por \(V \oplus W\). O produto cartesiano é formado por duplas \(\big( \ket{v} , \ket{w} \big)\), com \(\ket{v} \in V\) e \(\ket{w} \in W\). Nesta subseção, a notação \(( \cdot \, , \cdot )\) refere-se a par ordenado em vez de produto interno como no restante do texto.
As diferenças entre essas duas operações estão dispostas no que segue:
Produto Tensorial |
Produto Cartesiano ou Soma Direta |
|
|---|---|---|
Notação: |
\(V \otimes W\) |
\(V \times W = V \oplus W\) |
Base: |
\(\ket{v_k} \otimes \ket{w_l}\) |
\(\big( \ket{v_k} , 0 \big) \ , \ \big( 0 , \ket{w_l} \big)\) |
Dimensão: |
\(\dim V \otimes W = \dim V \cdot \dim W\) |
\(\dim V \oplus W = \dim V + \dim W\) |
Outra diferença é que a soma, no produto cartesiano, é uma soma entrada a entrada
enquanto que a soma no produto tensorial, de modo geral, não se reduz
a não ser que, por exemplo, \(\ket{v^1} = \ket{v^2}\), de modo que
A multiplicação por escalar no produto cartesiano também é entrada a entrada
enquanto que, no produto tensorial, o escalar pode ser incorporado a qualquer das duas entradas, mas deve ir para apenas uma delas
Produto Interno#
Sejam \(V\) e \(W\) espaços de Hilbert, isto é, espaços munidos de produto interno. O produto tensorial \(V\otimes W\) pode ser munido com um produto interno derivado dos produtos internos de \(V\) e de \(W\). Defina:
estendendo a definição para elementos arbitrários do produto tensorial por linearidade na segunda entrada e antilinearidade na primeira.
Para dois vetores da forma \(\ket{v^1}\otimes \ket{w^1}\) e \(\ket{v^2}\otimes \ket{w^2}\) do produto tensorial, pode-se denotar
e decorre da definição de produto interno que
Exemplo
O espaço vetorial \(\mathbb{C}^2 \otimes \mathbb{C}^2\) que descreve 2 qubits foi apresentado no exemplo Espaço Vetorial de 2 Qubits. O produto interno nesse espaço é explicitado no que segue. Use os índices \(A\) e \(B\) para fazer referência à primeira e à segunda entrada tensorial, respectivamente.
O produto interno dos vetores da base é dado pela equação Produto Interno de Vetores da Base, que se traduz em
em que \(j,k,p,q = 0,1\). Por exemplo,
Sejam
O produto interno de \(\ket{\phi}\) com \(\ket{\psi}\) é dado por
A norma de \(\ket{\phi}\) é dada por
Exemplos:
Operadores#
Sejam \(A\) um operador em \(V\) e \(B\) um operador em \(W\). É possível definir um operador em \(V\otimes W\), denotado por \(A\otimes B\) de forma que
Todo operador em \(V \otimes W\) pode ser decomposto em uma combinação linear de operadores da forma apresentada anteriormente.
Pode-se mostrar que a composição, ou produto, de dois operadores \(A \otimes B\) e \(A' \otimes B'\) é dada por:
Exemplo
Sejam \(X\) e \(H\) operadores no espaço de 1 qubit dados por
Esses operadores foram utilizados em vários dentre os exemplos anteriores.
O operador \(H \otimes X\) atua no espaço de 2 qubits como no exemplo abaixo.
Se forem usados rótulos \(1\) e \(2\) para as entradas tensoriais, a conta do exemplo acima poderia ser reescrita como
Mais detalhes sobre a notação encontram-se na seção Produto Tensorial: Notação.
Produto de Kronecker#
Até então, o conceito de produto tensorial foi apresentado de maneira abstrata. É possível abordar esse conceito de maneira matricial também. Fixadas bases para \(V\) e \(W\), os vetores \(\ket{v}\) e \(\ket{w}\) desses espaços podem ser representados como vetores coluna. O vetor \(\ket{v} \otimes \ket{w}\) também pode ser representado como vetor coluna fazendo-se o produto de Kronecker.
Essa operação é mais facilmente compreendida por meio de um exemplo.
Exemplo
O produto tensorial de operadores em \(V\) e \(W\) também pode ser obtido matricialmente por meio do produto de Kronecker.
Exemplo
O produto de Kronecker, em geral, não é comutativo.
Se \(A \in M(m_A,n_A)\) e \(B \in M(m_B, n_B)\), então a matriz \(A \otimes B\) tem \(m_Am_B\) linhas e \(n_An_B\) colunas, ou seja, \(A\otimes B \in M(m_Am_B,n_An_B)\). Uma forma geral de escrever o elemento \(j,k\) da matriz \(A\otimes B\) é
em que
e, para \(x,y\) inteiros,
Exemplo
\(A_{2\times2}\) , \(B_{3\times2}\). O elemento \(4,2\) da matriz \(A\otimes B\) pode ser obtido por:
Produto Tensorial de Vários Espaços Vetoriais#
O produto tensorial de vários espaços vetoriais segue a mesma ideia do caso de dois espaços, apresentado anteriormente. A dimensão será o produto das dimensões de cada espaço. O produto tensorial é associativo, então não é necessário usar parênteses num produto tensorial de vários espaços. Não é possível comutar os fatores do produto tensorial.
Notação#
Em situações práticas, costuma-se usar índices em cada fator do produto tensorial para evitar confusões. Também há variantes que deixam a notação mais curta. Alguns comentários a respeito dessas variantes são abordados nesta seção. Para tratar disso, considere um exemplo em \(V\otimes W \otimes U\).
Pode-se denotar um elemento da forma \(\ket{v} \otimes \ket{w} \otimes \ket{u}\) omitindo-se o símbolo \(\otimes\): \(\ket{v} \ket{w} \ket{u}\). Nesse caso, deve-se tomar cuidado para não confundir essa justaposição com o produto matricial; nas situações de interesse, normalmente o produto matricial não será possível e há menos risco de confusão.
Costuma-se atribuir índices aos fatores: \(\ket{v} \otimes \ket{w} \otimes \ket{u} = \ket{v}_V \otimes \ket{w}_W \otimes \ket{u}_U = \ket{v}_V \ket{w}_W \ket{u}_U\). Ainda, pode-se escrever esse elemento como: \(\ket{v}_1 \ket{w}_2 \ket{u}_3\), ou \(\ket{v \, w \, u}_{VWU}\), ou, ainda, qualquer notação equivalente, que evidencie a que espaço cada ket pertence. Com a identificação por índices, é possível até trocar a ordem em que são escritos; não deve ser confundido com a comutatividade dos fatores, que não é permitida em geral. Assim, pode-se escrever: \(\ket{u}_3 \ket{w}_2 \ket{v}_1\).
Os bras também podem ser rotulados com índices. Por exemplo, escreve-se \(\big( \ket{v}_1 \ket{w}_2 \ket{u}_3\big)^\dagger = {}_1\bra{v} {}_2\bra{w} {}_3\bra{u}\), ou \(\ket{v \, w \, u}_{VWU}^{\ \ \dagger} = {}_{VWU}\bra{v \, w \, u}\).
Considere, agora, os operadores da forma \(A\otimes B\otimes C\), com \(A\), \(B\) e \(C\) operadores nos espaços \(V\), \(W\) e \(U\), respectivamente. É possível também atribuir índices nos operadores para lembrar em que espaço cada um deles atua. Por exemplo, pode-se denotar: \(A_1\otimes B_2\otimes C_3\).
Há situações em que se deseja operar apenas em uma das entradas do produto tensorial. Assim, por exemplo, \(A\ket{v} \otimes \ket{w}\otimes \ket{u} = A_1 \big( \ket{v} \otimes \ket{w}\otimes \ket{u} \big)\). Formalmente, \(A_1 = A \otimes I \otimes I\), nesse caso. O produto (ou composição) dos operadores \(A_1 B_2 C_3\) significa \((A\otimes I \otimes I) (I \otimes B \otimes I)(I \otimes I \otimes C) = AII \otimes IBI \otimes IIC = A\otimes B \otimes C\). Dessa forma, com os índices, pode-se escrever \(A_1 B_2 C_3 = A \otimes B \otimes C\) sem perigo de confusão com o produto matricial de \(A\), \(B\) e \(C\); Pode-se até mesmo trocar a ordem de como são escritos: \(B_2 A_1 C_3 = A\otimes B \otimes C\).
Outra notação bastante utilizada é quando se deseja realizar o produto tensorial entre \(n\) cópias de um vetor \(\ket{\psi}\). Define-se
Essa notação pode ser utilizada para bras e para operadores: \(\bra{\psi}^{\otimes n}\), \(A^{\otimes n }\). Também é possível usar uma notação análoga ao produtório para denotar, por exemplo,
Há, pois, diversas maneiras de se denotar os mesmos vetores ou operadores. Essa variedade é útil para permitir a escrita de expressões compactas em diversas situações em que o produto tensorial aparece.