Show code cell source Hide code cell source

!pip install ket-lang
!pip install numpy
import numpy as np
Import math
from ket import *

Algoritmo de Busca de Grover

Esta seção aborda o Algoritmo de Grover, um algoritmo quântico que permite encontrar um elemento em uma lista não ordenada. Uma descrição mais rigorosa desse problema, bem como as alternativas clássicas para o mesmo são apresentadas neste texto.

Problema de Grover

O problema de Grover consiste em encontrar um elemento específico em uma lista de \(2^n\) itens. A lista é formada por palavras binárias de \(n\) dígitos. Há uma função booleana \(f\colon \{ 0,1 \}^n \to \{ 0,1 \}\) que só sinaliza ‘1’ para uma entrada \(x_0\) em particular, que pode ser desconhecida. Em outras palavras, a função \(f\) pode ser descrita por

\[\begin{split} 0 \ , \ x \neq x_0 \\ 1 \ , \ x = x_0 \ \end{split}\]

A maneira de saber se o item \(x\) considerado corresponde ao desejado é por meio da aplicação de \(f\). Essa função poderia ser chamada de ``teste’’, e caso se queira saber se o item \(x\) da lista é o desejado (em outras palavras, se \(x = x_0\)), deve-se fazer o teste em \(x\) e ver se o teste resulta em ‘1’ (item desejado foi encontrado) ou ‘0’ (o item testado não é o desejado).

Problema de Grover

Encontrar a única entrada \(x_0 \in \{ 0,1 \}^n\) tal que o resultado do teste \(f\) sinaliza ‘1’. Ou seja, encontrar único \(x_0\) com

\[f(x_0) = 1 \ . \]

Em seguida, um algoritmo quântico é apresentado para resolver o problema de forma mais eficiente do que seria possível classicamente.

Algoritmo de Grover

O algoritmo de Grover é um algoritmo quântico para resolução do problema de Grover, que consiste em encontrar o elemento em uma lista por meio de um teste \(f\), e o elemento desejado é o único \(x_0\) que faz com que o teste sinalize 1. O algoritmo quântico consiste em aplicar uma subrotina quântica, o operador de Grover, por um número de vezes da ordem de \(\sqrt{N}\), em que \(N=2^n\) é o número de itens na lista, indexados por \(n\) bits.

Algoritmo de Grover

Entrada: \(O_\text{F}(f) = O\) \ (oráculo de fase associado à função booleana \(f\))

Procedimento:

\[\begin{split} \begin{array}{lll} \text{etapa 0:} & \ket{0}^{\otimes n} & \text{preparação do estado inicial} \\ \text{etapa 1:} & H^{\otimes n}\ket{0}^{\otimes n} & \text{superposição dos estados na base computacional} \\ \text{etapa 2:} & G & \text{aplicação do operador de Grover} \\ \text{etapa 3:} & \text{repetir etapa 2 por $k$ vezes, com} \\ & k = \dfrac{acos(\frac{1}{\sqrt{N}})}{acos(\frac{N-2}{N})} \ , \ \ N = 2^n \ . \end{array} \end{split}\]

\[\begin{split} \begin{array}{lll} \text{etapa 1:} & O_\text{F}\ket{+}^{\otimes n} & \text{aplicação de $f$ (oráculo de fase)} \\ \text{etapa 2:} & H^{\otimes n} & \\ \text{etapa 3:} & 2\ket{0}\bra{0} - I & \\ \text{etapa 4:} & H^{\otimes n} & \\ \end{array} \end{split}\]

Saída: Leitura do registrador fornece o item \(x_0\) buscado, com probabilidade de acerto

\[ P_a >\frac{N-1}{N} , \ \ N = 2^n \ . \]

EXERCÍCIO

Circuito

Notação compacta

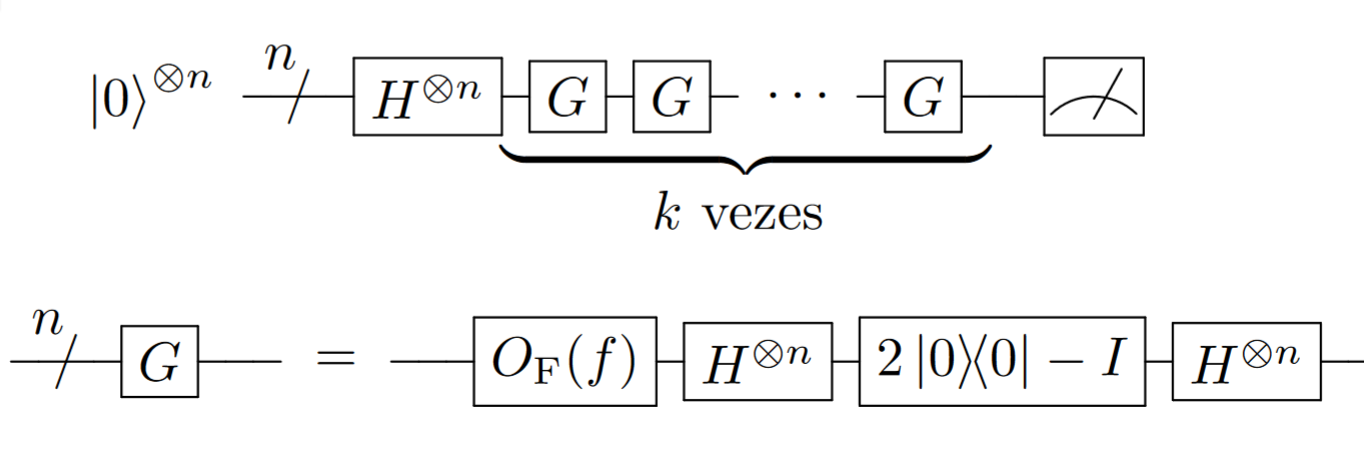
Notação auxiliar

Para facilitar, lista-se abaixo a notação utilizada nesse algoritmo:

\[ \ket{0} = \ket{0 \ldots 0} = \ket{0}^{\otimes n} \]

\[[ \ket{\psi} := \ket{+}^{\otimes n} \]

\[\mathbb{B}_n : \text{ conjunto de todas as palavras de $n$ bits} \]

\[\begin{split} N := 2^n \ \ \begin{cases} \text{$n$: número de qubits de cada item da lista} \\ \text{$N$: número de itens na lista } \end{cases} \end{split}\]

\[\begin{split} \ket{\alpha} := \sum_{\scriptsize \begin{array}{c} x \in \mathbb{B}_n \\ x \neq x_0 \end{array}} \frac{\ket{x}}{\sqrt{N-1}} \end{split}\]

\[ \ket{\beta} := \ket{x_0} \text{: item desejado na lista} \]

\[ S := \text{span}_\mathbb{R} \{ \ket{\alpha} , \ket{\beta} \} \text{: espaço vetorial gerado por $\ket{\alpha}$, $\ket{\beta}$ com escalares reais} \]

Contas auxiliares

Vale que:

\[\begin{split} \begin{split} \ket{\psi} &= \ket{+}^{\otimes n} \\ &= \sum_{x \in \mathbb{B}_n} \frac{\ket{x}}{\sqrt{N}} \\ &= \frac{\sqrt{N-1}}{\sqrt{N}} \sum_{\scriptsize \begin{array}{c} x \in \mathbb{B}_n \\ x \neq x_0 \end{array}} \frac{\ket{x}}{\sqrt{N-1}} \ \ + \ \ \frac{\ket{x_0}}{\sqrt{N}} \\ &= \frac{\sqrt{N-1}}{\sqrt{N}} \ket{\alpha} + \frac{1}{\sqrt{N}} \ket{\beta} \end{split} \end{split}\]

A aplicação de \(O_\text{F}\) em \(\ket{\alpha}\) e \(\ket{\beta}\) fica:

\[\begin{split} \begin{split} O_\text{F} \ket{\alpha} &= O_\text{F}\sum_{\scriptsize \begin{array}{c} x \in \mathbb{B}_n \\ x \neq x_0 \end{array}} \frac{\ket{x}}{\sqrt{N-1}} \\ &= \sum_{\scriptsize \begin{array}{c} x \in \mathbb{B}_n \\ x \neq x_0 \end{array}}\frac{1}{\sqrt{N-1}} O_\text{F}\ket{x} \\ &= \sum_{\scriptsize \begin{array}{c} x \in \mathbb{B}_n \\ x \neq x_0 \end{array}}\frac{1}{\sqrt{N-1}} \ket{x} \\ &= \ket{\alpha} \ , \end{split} \end{split}\]

\[\begin{split} \begin{split} O_\text{F} \ket{\beta} &= O_\text{F} \ket{x_0} \\ &= - \ket{x_0} \\ &= - \ket{\beta} \ . \end{split} \end{split}\]

O operador \(G\) pode ser escrito como:

\[\begin{split} \begin{split} G &= H^{\otimes n} (2\ket{0}\bra{0} - I) H^{\otimes n} O_\text{F} \\ &= \big(2H^{\otimes n}\ket{0}\bra{0}H^{\otimes n} - H^{\otimes n}I H^{\otimes n} \big)O_\text{F} \\ &= \big(2H^{\otimes n}\ket{0}\bra{0}(H^{\otimes n})^\dagger - H^{\otimes n} H^{\otimes n} \big)O_\text{F} \\ &= (2\ket{\psi}\bra{\psi} - I) O_\text{F} \ , \end{split} \end{split}\]

em que foi definido \(\ket{\psi} = \ket{+}^{\otimes n}\).

Primeira aplicação do operador \(G\)

Antes de aplicar o operador \(G\) pela primeira vez, prepara-se o estado inicial fazendo uma superposição com pesos iguais em cada qubit:

\[\begin{split} \begin{split} \ket{\psi_0} &= H^{\otimes n} \ket{0}^{\otimes n} \\ &= \ket{+}^{\otimes n} \\ &= \ket{\psi} \\ &= \frac{\sqrt{N-1}}{\sqrt{N}} \ket{\alpha} + \frac{1}{\sqrt{N}} \ket{\beta} \ \ \text{usando ($\psi$)} \ . \\ \end{split} \end{split}\]

Nota-se que \( \ket{\psi_0}\) pertence ao subespaço vetorial \(S\) gerado por \(\ket{\alpha},\ket{\beta}\) e com escalares reais. Isso permitirá uma interpretação geométrica muito útil para o entendimento do algoritmo.

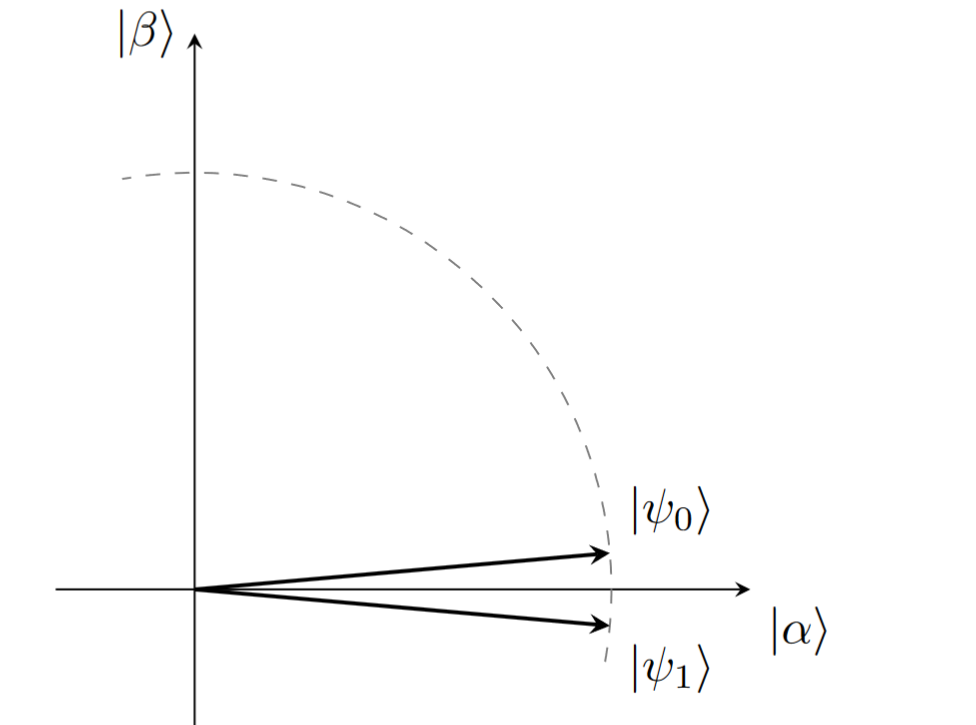
Na etapa 1 de \(G\), aplica-se o oráculo de fase ao estado inicial \(\ket{\psi}\):

\[\begin{split} \begin{split} \ket{\psi_1} &= O_\text{F} \ket{\psi_0} \\ &= O_\text{F} \left( \frac{\sqrt{N-1}}{\sqrt{N}} \ket{\alpha} + \frac{1}{\sqrt{N}} \ket{\beta} \right) \ \ \text{usando ($\psi$)} \\ &= \frac{\sqrt{N-1}}{\sqrt{N}} O_\text{F} \ket{\alpha} + \frac{1}{\sqrt{N}} O_\text{F} \ket{\beta} \\ &= \frac{\sqrt{N-1}}{\sqrt{N}} \ket{\alpha} - \frac{1}{\sqrt{N}} \ket{\beta} \ \ \text{usando ($\alpha$) e ($\beta$)} \end{split} \end{split}\]

O vetor \(\ket{\psi_1}\) continua no espaço \(S\), e a aplicação do oráculo de fase pode ser visualizada como uma reflexão em torno do eixo \(\ket{\alpha}\).

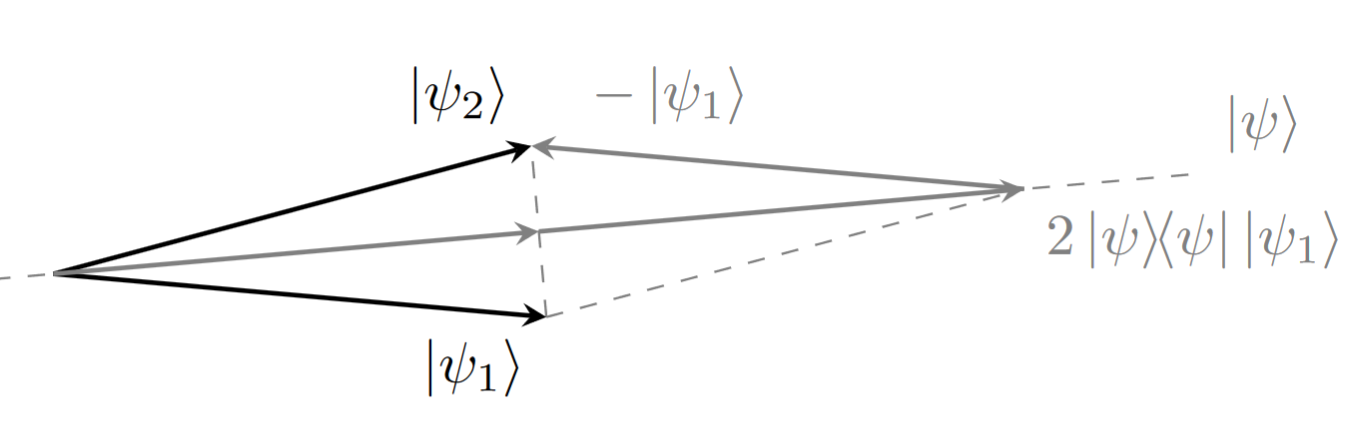
As etapas 2, 3 e 4 de \(G\) redundam em aplicar \(2 \ket{\psi}\bra{\psi} - I\) em \( \ket{\psi_1} \), conforme equação (\(G\)). E a aplicação desse operador pode ser vista geometricamente de acordo com a figura abaixo.

\[\begin{split} \begin{split} \ket{\psi_2} &= (2 \ket{\psi}\bra{\psi} - I) \ket{\psi_1} \\ &= 2 \ket{\psi}\bra{\psi}\ket{\psi_1} - \ket{\psi_1} \end{split} \end{split}\]

Dessa forma, a primeira aplicação do operador \(G\) fornece o seguinte.

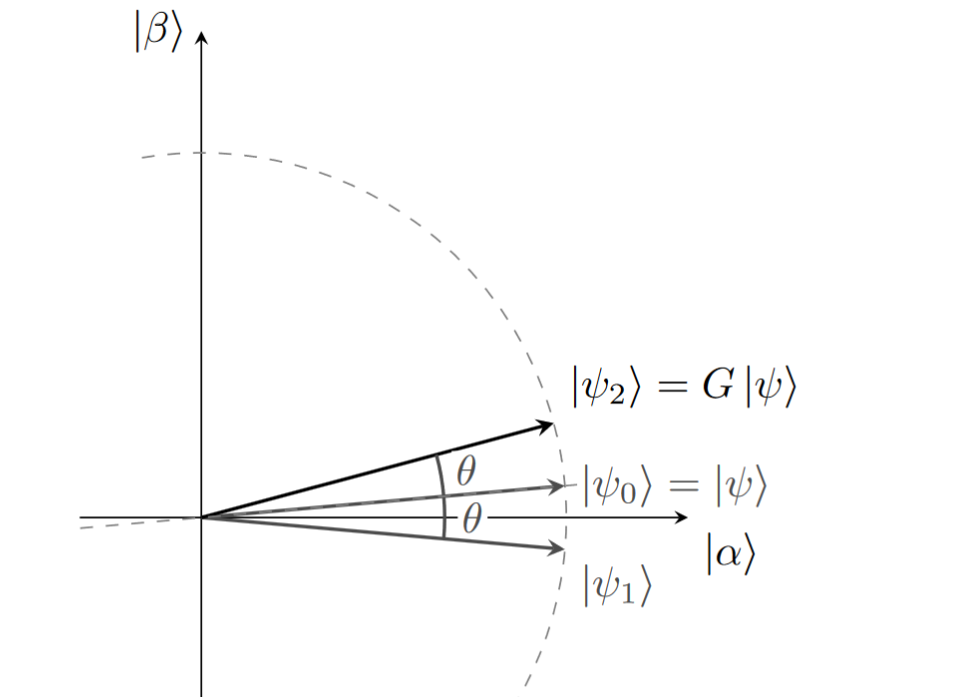
EXERCÍCIO

Aplicações subsequentes do operador \(G\)

As aplicações sucessivas do operador de Grover têm o mesmo efeito descrito anteriormente. Cada aplicação de \(G\) corresponde a uma rotação no sentido anti-horário. A figura a seguir ilustra a \(l\)-ésima aplicação de \(G\).

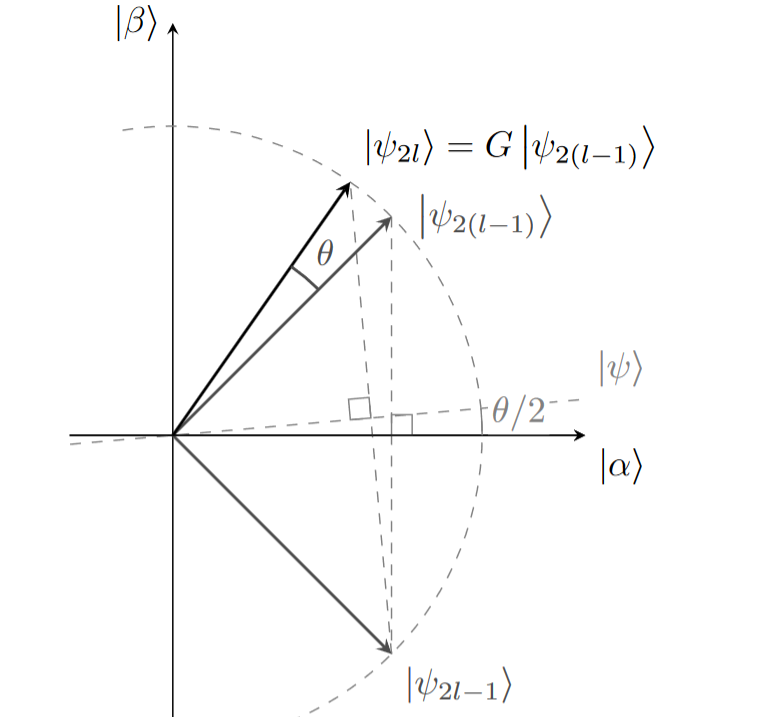
O operador \(G\) é aplicado por \(k\) vezes até que o vetor resultante esteja o mais próximo possível do eixo \(\ket{\beta}\).

Número necessário de aplicações de \(G\)

O número de aplicações \(k\) necessário é dado por

\[ k \theta + \frac{\theta}{2} = \frac{\pi}{2} \implies k = \frac{\pi - \theta}{2\theta} \ , \]

em que se arredonda \(k\) para o inteiro mais próximo.

O ângulo \(\theta\) (em radianos) é o ângulo que \(G\ket{\psi}\) faz com \(\ket{\psi}\). Pode ser obtido por:

\[\begin{split} \begin{split} \cos \frac{\theta}{2} &= \braket{\beta}{\psi} = \frac{\sqrt{N-1}}{\sqrt{N}} \qquad \text{usando ($\psi$)} \\ \sin \frac{\theta}{2} &= \sqrt{1 - |\braket{\beta}{\psi}}^2| = \frac{1}{\sqrt{N}} \end{split} \end{split}\]

Fazendo-se a seguinte manipulação algébrica, pode-se encontrar outra expressão equivalente para o ângulo.

\[\begin{split} \begin{split} \ket{\psi_1} &= \frac{\sqrt{N-1}}{\sqrt{N}} \ket{\alpha} - \frac{1}{\sqrt{N}} \ket{\beta} \\ &= \frac{\sqrt{N-1}}{\sqrt{N}} \ket{\alpha} + \frac{1}{\sqrt{N}} \ket{\beta} - \frac{2}{\sqrt{N}} \ket{\beta} \\ &= \ket{\psi} - \frac{2}{\sqrt{N}} \ket{\beta} \qquad \text{usando ($\psi$)} \phantom{xxxxxxxxxxxxxxxxx} \end{split} \end{split}\]

\[\begin{split} \begin{split} \ket{\psi_2} &= G \ket{\psi} \\ &= \big( 2 \ket{\psi}\bra{\psi} - I \big)\ket{\psi_1} \\ &= \big( 2 \ket{\psi}\bra{\psi} - I \big)\left( \ket{\psi} - \frac{2}{\sqrt{N}}\ket{\beta} \right) \\ &= 2\ket{\psi}\braket{\psi}{\psi} - \ket{\psi} - \frac{4}{\sqrt{N}}\ket{\psi}\braket{\psi}{\beta} + \frac{2}{\sqrt{N}}\ket{\beta} \\ &= 2\ket{\psi} - \ket{\psi} - \frac{4}{\sqrt{N}} \frac{1}{\sqrt{N}}\ket{\psi} + \frac{2}{\sqrt{N}}\ket{\beta} \qquad \text{usando ($\psi$)} \\ &= \frac{N-4}{N} \ket{\psi} + \frac{2}{\sqrt{N}}\ket{\beta} \\ % &= \frac{N-4}{N} \left( \frac{\sqrt{N-1}}{\sqrt{N}} \ket{\alpha} + \frac{1}{\sqrt{N}} \ket{\beta} \right) + \frac{2}{\sqrt{N}}\ket{\beta} \\ % &= \frac{(N-4)\sqrt{N-1}}{N\sqrt{N}}\ket{\alpha} + \frac{N-2}{N\sqrt{N}} \ket{\beta} \end{split} \end{split}\]

\[\begin{split} \begin{split} \cos \theta &= \braket{\psi}{G\psi} \\ &= \bra{\psi} \left(\frac{N-4}{N} \ket{\psi} + \frac{2}{\sqrt{N}}\ket{\beta} \right) \\ % & \qquad \qquad \qquad \text{usando ($\ast$)} \\ &= \frac{N-4}{N} \braket{\psi}{\psi} + \frac{2}{\sqrt{N}}\braket{\psi}{\beta} \\ &= \frac{N-4}{N} + \frac{2}{\sqrt{N}}\frac{1}{\sqrt{N}} \qquad \text{usando ($\psi$)} \\ &= \frac{N-2}{N} \ . % \phantom{xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxi} \end{split} \end{split}\]

Portanto, pode-se escrever

\[ \theta = 2acos(\frac{\sqrt{N-1}}{\sqrt{N}}) = 2asin(\frac{1}{\sqrt{N}}) = acos(\frac{N-2}{N}) \ , \]

e o valor de \(k\) é dado por

\[ k = \frac{\pi - \theta}{2\theta} = \frac{\pi - acos(\frac{N-2}{N})}{2acos(\frac{N-2}{N})} \]

ou por

\[ k = \frac{\frac{\pi}{2} - \frac{\theta}{2}}{\theta} = \frac{\frac{\pi}{2} - asin(\frac{1}{\sqrt{N}})}{acos(\frac{N-2}{N}) } = \frac{acos(\frac{1}{\sqrt{N}})}{acos(\frac{N-2}{N})} \ . \]

É possível verificar que o número \(k\) é da ordem de \(\sqrt{N}\). Tem-se

\[ \lim_{N\to +\infty} k = +\infty \]

\[ \lim_{N\to +\infty} \frac{k}{\sqrt{N}} = \frac{\pi}{4} \]

\[ \lim_{N\to +\infty} \frac{k}{N} = 0 \ . \]

Probabilidade de acerto

Ao aplicar a subrotina \(G\) por um número \(k\) de vezes especificado anteriormente, obtém-se o estado final o mais próximo possível de \(\ket{\beta} = \ket{x_0}\), o item desejado. A projeção na direção desse vetor permite encontrar a probabilidade de acerto do algoritmo. O estado final \(G^k \ket{\psi}\) faz um ângulo com o estado \(\ket{x_0}\) menor que \(\theta/2\), pois se fosse maior ou igual, seria possível aplicar novamente o operador \(G\) para reduzi-lo. Portanto, o ângulo \(\cos \theta\big(\ket{x_0},G^k\ket{\psi}\big)\) entre o estado desejado e o estado final é menor que \(\theta/2\), o que significa que seu cosseno é maior que \(\cos (\theta/2)\).

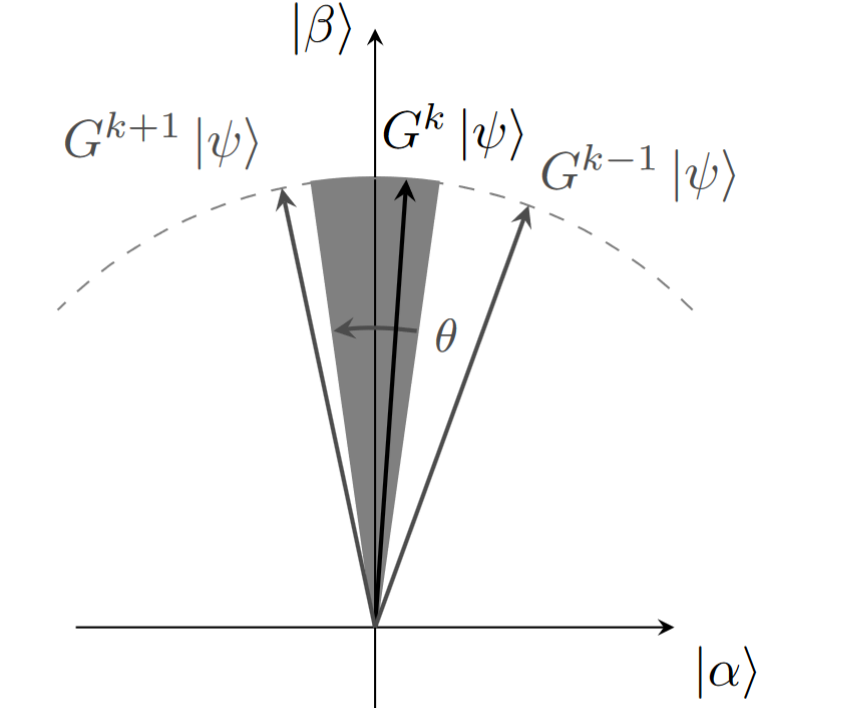
Com isso, tem-se a probabilidade de acerto estimada em

\[\begin{split} \begin{split} P_a &= ||\ket{x_0}\bra{x_0}G^k \ket{\psi}||^2 \\ &= |\braket{x_0}{G^k\ket{\psi}}|^2 \\ &= |\cos \theta\big(\ket{x_0},G^k\ket{\psi}\big)|^2 \\ &> |\cos \theta/2|^2 \\ &= \left(\frac{\sqrt{N-1}}{\sqrt{N}}\right)^2 \\ &= \frac{N-1}{N} \ , \ \ N = 2^n \ . \end{split} \end{split}\]

Generalização

O algoritmo de Grover também funciona para o caso em que há mais de um elemento marcado, isto é, há \(x_0\), \(x_1\), \(\ldots\), \(x_{m-1}\) elementos tais que \(f(x_0) = f(x_1) = \ldots = f(x_{m-1})\) e os demais valores anulam \(f\). É possível adaptar a análise do algoritmo para esse caso. A interpretação geométrica continua valendo, mas desta vez, tem-se

\[\begin{split} \ket{\alpha} = \frac{1}{\sqrt{N-m}} \sum_{\scriptsize \begin{array}{c} x \in \mathbb{B}_n \\ f(x) = 0 \end{array} } \ket{x} \end{split}\]

\[\begin{split} \ket{\beta} = \frac{1}{\sqrt{m}} \sum_{\scriptsize \begin{array}{c} x \in \mathbb{B}_n \\ f(x) = 1 \end{array} } \ket{x} \ . \end{split}\]

EXERCÍCIO

Algoritmo Clássico

Algoritmo Clássico Determinístico

Classicamente, se o teste é dado como uma caixa preta, em que não se sabe a estrutura interna de \(f\), a maneira de se encontrar \(x_0\) é por busca exaustiva. Para garantir que o item \(x_0\) seja encontrado, deve-se, no pior caso, olhar todas as \(N = 2^n\) entradas possíveis. Portanto são necessários \(N\) aplicações do teste \(f\).

Algoritmo Clássico Probabilístico

Considere um algoritmo que sorteie aleatoriamente as entradas a serem testadas (e sem repetir entradas). Após o teste de \(k\) entradas, a probabilidade de que se tenha localizado o item desejado \(x_0\) é de

\[ P = \frac{k}{N} \ . \]

Para que haja probabilidade de encontrar a resposta seja maior que \(1/2\), deve-se testar pelo menos por um número de vezes

\[ k > \frac{N}{2} \ . \]

Desse modo, ainda deve-se aplicar o teste \(f\) da ordem de \(N\) vezes.

\begin{subsection}{Comparação de Desempenho}
O desempenho dos algoritmos são comparados na tabela abaixo.

Dessa forma, o algoritmo de Grover apresentaria ganho quadrático de desempenho em relação aos algoritmos clássicos, se a aplicação de \(f\) nos casos clássico e quântico forem equivalentes em termos de custos computacionais.

Simulação do algorítimo de Grover

Para simular o algorítimo de Grover usaremos a línguagem Ket de computação quântica, para isso precisamos ter a mesma instalada, caso não possua o pacote instalado rode o seguinte código:

pip install ket-lang

Com a biblioteca instalada, importa-se a mesma para ser usada dentro do seu código:

from ket import *

Primeiro iremos inicializar o oráculo:

def oracle(qubits, target):
    """Oráculo: inverte a amplitude do estado desejado."""
    X(
        qubits[i]
        for i, bit in enumerate(bin(target)[2:].zfill(len(qubits)))
        if bit == "0"
    )
    H(qubits[-1])
    ctrl(qubits[:-1], X, qubits[-1])  # Controle multi-qubit
    H(qubits[-1])
    X(
        qubits[i]
        for i, bit in enumerate(bin(target)[2:].zfill(len(qubits)))
        if bit == "0"
    )

Em seguida o operador de difusão

def diffusion_operator(qubits):
    """Operador de difusão: amplifica as amplitudes dos estados marcados."""
    H(qubits)
    X(qubits)
    H(qubits[-1])
    ctrl(qubits[:-1], X, qubits[-1])  # Controle multi-qubit
    H(qubits[-1])
    X(qubits)
    H(qubits)

Por fim aplicamos o algorítimo de Grover utilizando-se das portas quânticas já conhecidas, do oráculo e do operador de difusão:

def grover(n, target):
    """Executa o algoritmo de Grover."""
    # Inicialização do processo
    process = Process()

    # Alocação de n qubits
    qubits = process.alloc(n)

    # Superposição inicial
    H(qubits)

    # Número ideal de iterações: sqrt(2^n)
    iterations = int((2**n) ** 0.5)

    # Iterações do algoritmo de Grover
    for _ in range(iterations):
        oracle(qubits, target)
        diffusion_operator(qubits)

    # Medição
    result = [measure(q).value for q in qubits]
    print("Estado encontrado:", result)