Show code cell source
!pip install -U -q pip
!pip install -U -q 'ket-lang[full]>=0.8.3,<0.9'
from IPython.display import display
import plotly.io as pio
pio.renderers.default = "iframe"
Programacão Quântica com Ket#
Neste capítulo, exploraremos a plataforma de programação quântica Ket, um projeto de código aberto que permite desenvolver e testar aplicações quânticas.
Introdução#
Instalação#
Se você estiver executando esta página com Live Code, o Ket será instalado automaticamente quando o ambiente de execução for carregado. Caso esteja utilizando um Notebook baixado desta página ou acessando via Binder/Colab, os comandos de instalação estarão na primeira célula do notebook.
Para integrar o Ket em um projeto externo, instale-o via PyPI utilizando o seguinte comando:
pip install -U pip
pip install ket-lang
Documentação#
A documentação completa da API do Ket está disponível em quantumket.org. Caso tenha dúvidas sobre alguma função ou queira conhecer as funcionalidades disponíveis, recomendamos a consulta à documentação. Além disso, todas as classes, métodos e funções referenciados nesta página possuem links diretos para suas respectivas documentações. Sempre que encontrar um novo elemento, sugerimos a leitura do material correspondente para uma compreensão mais detalhada.
Importando o Ket#
A célula abaixo importa todas as funcionalidades do Ket, permitindo o acesso direto a todas as suas classes e funções:
from ket import *
from ket import lib as qulib
Processo Quântico#
Por trás de toda execução quântica no Ket, há um processo quântico, uma instância da classe Process. Ele é responsável por gerenciar desde a alocação dos qubits até a compilação do código quântico.
Para iniciar uma execução quântica, é necessário instanciar um Process. Existem diversas configurações que podem ser ajustadas, mas um bom ponto de partida é utilizar o construtor padrão. Se nenhum argumento for passado, o simulador KBW Sparse será utilizado com 32 qubits, e a execução dinâmica (live execution) será ativada por padrão.
Exploraremos o significado de cada parâmetro mais adiante neste capítulo.
Abaixo, temos a criação de um processo:
processo = Process()
Alocação de Qubits#
Na computação quântica, a unidade básica de computação é o qubit. No Ket, o elemento fundamental da programação é a classe Quant, que nada mais é do que uma lista de qubits. Toda operação quântica, seja a aplicação de portas lógicas ou medições, é realizada sobre um objeto do tipo Quant.
Em breve, veremos como aplicar essas operações nos qubits, mas primeiro, vamos entender como instanciá-los.
No Ket, um qubit está sempre associado a um Process. Para acessar qubits, é necessário fazer uma chamada de alocação para o processo quântico, utilizando o método alloc(). O resultado dessa alocação é uma lista de qubits encapsulada em um objeto Quant. Mesmo que apenas um qubit seja alocado, ele ainda estará dentro de um Quant.
Em muitos casos, um processo quântico é criado apenas para alocar qubits. No entanto, ele também armazena metadados (get_metadata()), que podem ser úteis para experimentos e análises.
Nota
Dentro de um Quant, os qubits são referências opacas. Isso significa que eles não armazenam diretamente a informação quântica, mas sim uma referência a essa informação dentro do computador quântico. Além disso, os qubits expostos ao programador são qubits lógicos, que, após o processo de compilação, serão mapeados para qubits físicos no hardware quântico.
A classe Quant funciona como uma lista de qubits, e suas instâncias suportam as operações padrão do Python para listas. Por exemplo, é possível:
Indexar qubits usando colchetes
[].Concatenar dois objetos
Quantutilizando o operador de adição+.
Abaixo, temos exemplos de alocação de qubits:
# Instanciando um novo processo quântico
processo = Process()
# Alocação de um único qubit
qubits = processo.alloc()
# Alocação de dois qubits
par_qubit = processo.alloc(2)
# Acessando os qubits individualmente
primeiro_qubit = par_qubit[0]
segundo_qubit = par_qubit[1]
# Concatenando os qubits
qubits_concatenados = qubits + primeiro_qubit + segundo_qubit
# Mostrando os qubits alocados e concatenados
print("Qubit alocado:", qubits)
print("Par de qubits alocados:", par_qubit)
print("Qubits concatenados:", qubits_concatenados)
Qubit alocado: <Ket 'Quant' [0] pid=0x7fc863fab310>
Par de qubits alocados: <Ket 'Quant' [1, 2] pid=0x7fc863fab310>
Qubits concatenados: <Ket 'Quant' [0, 1, 2] pid=0x7fc863fab310>
Ao imprimir na tela uma variável do tipo Quant, podemos observar uma lista com os índices dos qubits que esse objeto referencia.
É importante notar que, ao indexarmos elementos em um Quant, mesmo que estejamos acessando apenas um qubit, o retorno sempre será outro objeto do tipo Quant. No Ket, os qubits estão sempre encapsulados em instâncias dessa classe.
Portas Lógicas Quânticas#
O Ket oferece um conjunto universal de portas lógicas quânticas, permitindo a descrição de qualquer computação quântica. Todas as portas implementadas no Ket estão disponíveis no módulo gates. Na documentação, é possível visualizar tanto a representação matricial das portas quanto seus efeitos.
Portas de 1 Qubit#
As portas quânticas são aplicadas diretamente a qubits encapsulados em objetos Quant. No Ket, os qubits são implementados como referências opacas, garantindo que a aplicação de portas quânticas não tenha efeitos colaterais no estado clássico do sistema, afetando apenas o estado quântico.
As portas implementadas no Ket seguem a convenção de nomes em letras maiúsculas. Por exemplo, as portas de Pauli incluem X(), Y() e Z(), enquanto a porta de Hadamard é representada por H().
Portas de Pauli e de Hadamard#
As portas de Pauli e a porta de Hadamard são fundamentais para muitos algoritmos quânticos. As portas de Pauli realizam rotações de 180º nos eixos X, Y e Z da esfera de Bloch. No entanto, essas portas, por si só, não são suficientes para gerar superposição. Para isso, utilizamos a porta de Hadamard, que transforma um qubit do estado \(\ket{0}\) ou \(\ket{1}\) para o estado de superposição:
Dica
Para visualizar o efeito das portas, podemos utilizar o comando:
dump(<qubits>).sphere()
A seguir, apresentamos um exemplo que demonstra a aplicação das portas de Pauli e da porta de Hadamard. Recomendamos que você execute este código e experimente modificar a aplicação das portas para entender melhor seus efeitos:
# Instanciando um novo do processo quântico
processo = Process()
# Alocação de um qubit
qubits = processo.alloc()
X(qubits) # Porta de Pauli X
Y(qubits) # Porta de Pauli Y
Z(qubits) # Porta de Pauli Z
H(qubits) # Porta de Hadamard
dump(qubits).sphere() # Mostra o Bloch Sphere
Portas Parametrizadas#
Além das portas de Pauli e da porta de Hadamard, o Ket também oferece portas de rotação e a porta de fase, que desempenham um papel essencial na construção de algoritmos quânticos.
As portas de rotação, como RX(), RY() e RZ(), realizam rotações controladas em torno dos eixos X, Y e Z, respectivamente. Essas portas permitem manipular o estado de um qubit de forma precisa e controlada.
Já a porta de fase, representada por PHASE(), aplica uma fase ao estado do qubit. Essas portas são chamadas de portas parametrizadas, pois recebem um parâmetro clássico (um número real, float), que controla a operação aplicada.
A porta RZ() e a PHASE() são equivalentes em termos de fase global, ou seja, ao analisarmos seu efeito na esfera de Bloch, não conseguimos distingui-las. No entanto, quando usadas em operações controladas, a fase global pode gerar diferenças no estado quântico.
A seguir, apresentamos um exemplo que demonstra a aplicação das portas parametrizadas. Recomendamos que você execute este código e experimente modificar os parâmetros das portas para compreender melhor seus efeitos:
# Instanciando um novo do processo quântico
processo = Process()
# Alocação de um qubit
qubits = processo.alloc()
# Aplicação das portas parametrizadas
RX(0.5, qubits) # Porta de rotação Rx com ângulo de 0.5 radianos
RY(0.2, qubits) # Porta de rotação Ry com ângulo de 0.2 radianos
RZ(2.3, qubits) # Porta de rotação Rz com ângulo de 2.3 radianos
PHASE(0.2, qubits) # Porta de fase com ângulo de 0.2 radianos
dump(qubits).sphere() # Mostra o Bloch Sphere
Concatenando Portas Quânticas#
Ao listar a aplicação de portas lógicas quânticas linha por linha, podemos inflar desnecessariamente o número de linhas de código, tornando o programa menos legível e mais difícil de entender. Para evitar esse problema, uma prática útil na implementação de algoritmos quânticos é a concatenação de portas lógicas, que permite expressar operações de forma mais concisa.
No Ket, existem duas maneiras de concatenar portas lógicas.
Encadeamento de chamadas de função#
Essa abordagem é recomendada quando o número de portas encadeadas não é muito grande. No entanto, o uso excessivo de parênteses pode comprometer a legibilidade do código. Como cada porta implementada no Ket retorna o próprio objeto Quant passado como parâmetro, podemos encadear as operações conforme mostrado no exemplo abaixo:
# Instanciando um novo do processo quântico
processo = Process()
# Alocação de um qubit
qubits = processo.alloc()
H(Z(H(qubits))) # Equivalente a:
# H(qubit)
# Z(qubit)
# H(qubit)
dump(qubits).sphere() # Mostra o Bloch Sphere
Concatenação de portas#
A segunda opção é utilizar a função cat(), que permite criar uma nova porta representando a concatenação das portas passadas como argumento.
Essa abordagem é especialmente útil em situações onde precisamos armazenar ou reutilizar uma sequência específica de operações quânticas. Ao criar uma nova porta quântica com cat(), podemos encapsular essa sequência de operações em uma única entidade. Isso torna o código mais modular, facilita a reutilização de blocos de operações e melhora a organização do programa.
# Instanciando um novo do processo quântico
processo = Process()
# Alocação de um qubit
qubits = processo.alloc()
porta_X = cat(H, Z, H) # Concatena portas
porta_X(qubits)
dump(qubits).sphere() # Mostra o Bloch Sphere
Para concatenar portas parametrizadas usando a função cat(), basta fornecer o argumento clássico correspondente. Quando apenas esse argumento é passado, a função cria uma nova porta com o parâmetro já aplicado.
from math import pi
# Instanciando um novo do processo quântico
processo = Process()
# Alocação de um qubit
qubits = processo.alloc()
porta_H = cat(RY(pi / 2), RX(pi))
porta_X = cat(porta_H, RZ(pi), porta_H)
porta_X(qubits)
dump(qubits).sphere() # Mostra o Bloch Sphere
Portas de 2 Qubits#
Para explorar todo o potencial da computação quântica, é necessário utilizar o entrelaçamento quântico, que requer o uso de portas que operam em dois qubits, como a CNOT(). Juntas com as portas de 1 qubit apresentadas anteriormente, a porta CNOT() forma um conjunto universal de portas lógicas quânticas. Além disso, o Ket oferece outras portas para facilitar a implementação de algoritmos quânticos, como SWAP(), RXX(), RYY() e RZZ().
Para exemplificar o uso de portas de 2 qubits, vamos criar um estado de Bell:
Para isso, podemos utilizar a porta CNOT().
Dica
Como a geração de entrelaçamento requer dois ou mais qubits, não podemos mais usar a dump(<qubits>).sphere(). No entanto, podemos utilizar a função dump(qubits).show() para imprimir o estado quântico com a combinação linear dos estados da base computacional.
# Instanciando um novo processo quântico
p = Process()
# Alocação de dois qubits
a, b = p.alloc(2)
# Aplicando a porta Hadamard em 'a' para criar superposição
H(a)
# Aplicando a porta CNOT controlada por 'a' e alvo 'b'
# para criar o estado de Bell
CNOT(a, b)
# Imprimindo o estado do sistema
dump(a + b).show()
Assim como ocorre com as portas de 1 qubit, também é possível oncatenar operações com portas de 2 qubits, como exemplificado no código abaixo, que prepara o estado de Bell:
# Instanciando um novo processo quântico
p = Process()
# Alocação de dois qubits
a, b = p.alloc(2)
# Aplicando a porta CNOT controlada por 'a' e alvo 'b'
# após a aplicação da porta Hadamard em 'a'
CNOT(H(a), b)
# Imprimindo o estado do sistema
dump(a + b).show()
Produto Tensorial de Portas#
É possível criar portas de múltiplos qubits utilizando o produto tensorial com a função kron(). Essa função aceita múltiplas portas como argumentos e gera uma nova porta lógica que opera em múltiplos qubits.
Podemos usar a função kron() em conjunto com a função cat() para criar uma nova porta de dois qubits que prepara um estado de Bell, como no exemplo abaixo:
# Instanciando um novo processo quântico
p = Process()
# Alocação de dois qubits
a, b = p.alloc(2)
# Concatenando as operações para preparar o estado de Bell
bell = cat(kron(H, I), CNOT)
bell(a, b)
# Imprimindo o estado do sistema
dump(a + b).show()
Neste exemplo, a operação kron(H, I) cria uma porta de dois qubits, aplicando a operação Hadamard em a e a operação identidade em b. Em seguida, a operação CNOT é aplicada como uma operação controlada entre a e b. Isso resulta na preparação do estado de Bell nos qubits a e b.
Aqui está o seu texto corrigido e aprimorado:
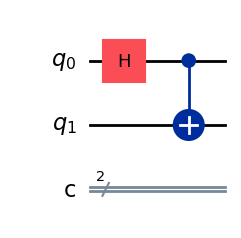
Como bell é considerada uma nova porta lógica quântica, podemos usar a função draw() para visualizar o circuito quântico que ela representa.
qulib.draw(gate=bell, num_qubits=(1, 1), output="mpl")
Instruções Quânticas#
Além das portas lógicas quânticas já apresentadas, o Ket oferece instruções que aproveitam a especificidade da computação quântica para facilitar a programação.
Operações Controladas#
É comum criar portas lógicas quânticas de múltiplos qubits adicionando qubits de controle a portas já existentes. No Libket, a biblioteca de tempo de execução do Ket, apenas portas de 1 qubit são implementadas, mas elas permitem a adição de controles. Por exemplo, podemos gerar a porta CNOT() a partir da porta X(). No Ket, as operações controladas são aplicadas somente se todos os qubits de controle estiverem no estado \(\ket{1}\).
Existem duas maneiras de realizar operações controladas no Ket:
Usando a instrução
withcontrol()para criar um contexto controlado.Utilizando a função
ctrl()para criar uma nova porta controlada.
Abaixo, apresentamos exemplos de como criar as portas CNOT, Toffoli (CCNOT), SWAP e Fredkin (CSWAP) a partir da porta X().
No Ket, qualquer função Python que aceite qubits como argumento e não realize nenhuma medida ou alocação de qubits pode ser considerada uma porta lógica quântica, o que facilita a criação de novas portas. Além disso, podemos usar a função draw() para visualizar a porta gerada.
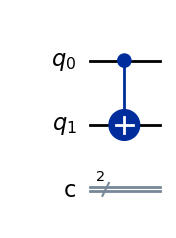
def meu_cnot(a, b):
ctrl(a, X)(b)
qulib.draw(gate=meu_cnot, num_qubits=(1, 1), output="mpl")
def meu_cnot2(a, b):
with control(a):
X(b)
qulib.draw(gate=meu_cnot2, num_qubits=(1, 1), output="mpl")

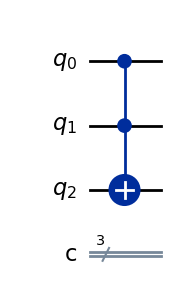
def toffoli(a, b, c):
ctrl(a + b, X)(c)
qulib.draw(gate=toffoli, num_qubits=(1, 1, 1), output="mpl")
def toffoli2(a, b, c):
with control(a + b):
X(c)
qulib.draw(gate=toffoli2, num_qubits=(1, 1, 1), output="mpl")

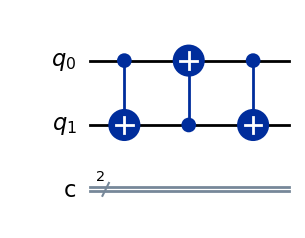
def meu_swap(a, b):
meu_cnot(a, b)
meu_cnot(b, a)
meu_cnot(a, b)
qulib.draw(gate=meu_swap, num_qubits=(1, 1), output="mpl")
Dica
Embora a implementação de meu_swap esteja correta, ela não aproveita uma otimização introduzida pelo uso de with around(), que será abordada mais adiante neste capítulo.
A ausência dessa otimização pode ser observada no circuito da porta Fredkin abaixo, que não está em sua forma otimizada.
def fredkin(a, b, c):
with control(a):
meu_swap(b, c)
qulib.draw(gate=fredkin, num_qubits=(1, 1, 1), output="mpl")
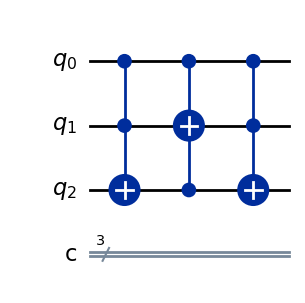
Exercício: Implementando o Estado GHZ#
Neste exercício, o objetivo é usar a função ctrl() para implementar uma porta quântica que prepara o estado GHZ de \(n\) qubits.
O estado GHZ é definido como:
Para implementar essa funcionalidade, você precisa completar a função ghz que recebe um objeto Quant representando os qubits e realiza as operações necessárias para preparar o estado GHZ.
def ghz(qubits: Quant):
# Implemente aqui a função ghz usando a função ctrl
...
n = 10
processo = Process()
qubits = processo.alloc(n)
ghz(qubits)
dump(qubits).show()
A função ctrl() recebe dois argumentos: um objeto do tipo Quant com os qubits de controle (sendo possível utilizar múltiplos qubits de controle) e uma função que atua como uma porta lógica quântica. É importante ressaltar que a função ctrl() não está limitada a adicionar qubits de controle apenas às portas quânticas disponíveis no módulo gates, mas pode adicionar qubits de controle a qualquer função. Por exemplo, podemos implementar uma porta de Bell e adicionar qubits de controle a ela como no código abaixo.
def bell(a: Quant, b: Quant) -> tuple[Quant, Quant]:
"""
Implementa a preparação do estado de Bell entre dois qubits.
Parâmetros:
a (Quant): O primeiro qubit.
b (Quant): O segundo qubit.
Retorna:
tuple[Quant, Quant]: Os qubits de entrada a e b.
Observação:
Por convenção, as portas implementadas no Ket retornam os Quants de
entrada para facilitar a concatenação de portas.
No entanto, isso não é necessário.
"""
H(a) # Aplica a porta Hadamard ao primeiro qubit
CNOT(a, b) # Aplica a porta CNOT controlada pelo primeiro qubit 'a' e alvo 'b'
return a, b # Retorna os qubits de entrada 'a' e 'b'
# Instancia um novo processo quântico
processo = Process()
# Aloca três qubits 'a', 'b' e 'c'
a, b, c = processo.alloc(3)
# Aplica uma operação controlada com o qubit 'a' e a função bell aos qubits 'b' e 'c'
ctrl(H(a), bell)(b, c)
# Imprime o estado do sistema
dump(a + b + c).show()
Operações Inversas#
Com exceção das operações de medida, toda computação quântica é reversível, ou seja, para todas as portas lógicas quânticas existe uma operação inversa correspondente. Isso é explorado em diversos algoritmos quânticos. Por exemplo, o algoritmo de estimação de fase requer uma operação de transformada de Fourier quântica inversa. No entanto, podemos implementar a transformada normalmente no Ket e usar a função adj() para criar a transformada inversa. Podemos ver isso em ação no código abaixo.
Dica
O código abaixo apresenta algumas operações que ainda não foram vistas neste capítulo. Não se preocupe em entender o código, o objetivo é apenas ilustrar o uso da função adj().
from math import pi
def qft(qubits: Quant, invert: bool = True):
if len(qubits) == 1:
H(qubits)
else:
*init, last = qubits
H(last)
for i, ctrl_qubit in enumerate(reversed(init)):
ctrl(ctrl_qubit, PHASE(pi / 2 ** (i + 1)))(last)
qft(init, invert=False)
if invert:
size = len(qubits)
for i in range(size // 2):
SWAP(qubits[i], qubits[size - i - 1])
def estimador_de_fase(oraculo, precisão: int) -> float:
assert precisão <= 20, "o tempo de computação pode ser muito grande"
p = Process(simulator="dense", num_qubits=precisão + 1)
ctr = H(p.alloc(precisão))
tgr = X(p.alloc())
for i, c in enumerate(ctr):
ctrl(c, oraculo)(i, tgr)
adj(qft)(ctr) # <- chada da transformada de Fourier quântica inversa
return measure(reversed(ctr)).value / 2**precisão
fase = pi
estimador_de_fase(
oraculo=lambda i, tgr: PHASE(2 * pi * (fase / 10) * 2**i, tgr),
precisão=18,
) * 10
3.1415939331054688
Para realizar operações inversas, uma abordagem alternativa é empregar a instrução with inverse(). Esta instrução cria um contexto onde as operações são executadas na ordem usual do Python, mas as portas lógicas quânticas são aplicadas de maneira inversa no estado quântico. Abaixo está um exemplo que demonstra o uso dessa instrução. Note que é necessário fornecer o Process onde as operações inversas serão aplicadas.
processo = Process()
a, b = processo.alloc(2)
print("Estado inicial:")
display(dump(a + b).show())
# Prepara o estado de Bell
H(a)
CNOT(a, b)
print("Estado após a preparação:")
display(dump(a + b).show())
# Invertendo a preparação do estado de Bell
with inverse(processo):
H(a)
CNOT(a, b)
print("Estado após a inversão da preparação:")
dump(a + b).show()
Estado inicial:
Estado após a preparação:
Estado após a inversão da preparação:
Operações \(UVU^\dagger\)#
Uma construção comum em algoritmos quânticos é aplicar uma operação \(U\) em torno de outra operação \(V\), seguida pela operação inversa \(U^\dagger\). Essa sequência de operações é representada matematicamente como \(UVU^\dagger\).
Um exemplo do uso desse tipo de construção está na implementação do difusor do algoritmo de Grover. Nele, uma operação controlada é envolta por portas de Hadamard. Aqui, as portas \(U\) são as portas de Hadamard, e é importante observar que a Hadamard é sua própria inversa. A porta controlada é representada pela porta \(V\).
def difusor(qubits: Quant, auxiliar: Quant):
with around(cat(H, X), qubits):
ctrl(qubits, X)(auxiliar)
fig = qulib.draw(gate=difusor, num_qubits=(3, 1), output="mpl")
fig.suptitle("Difusor do algoritmo de Grover")
fig
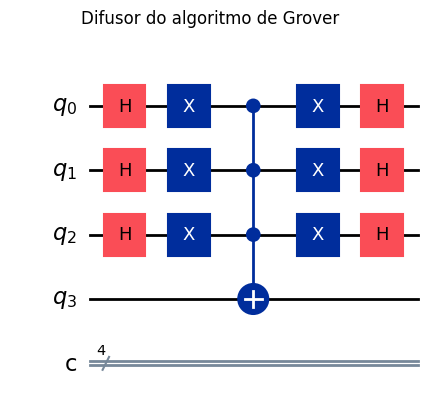
Para facilitar essa construção no Ket, a instrução with around() é oferecida. No exemplo acima, implementamos o difusor de Grover usando essa instrução.
A título de comparação, a seguir está implementado o difusor de Grover sem usar a instrução with around(). Além da redução do número de linhas, o uso de with around() torna o código mais legível e menos propenso a erros, proporcionando uma implementação mais eficiente.
def difusor_2(qubits: Quant, auxiliar: Quant):
H(qubits)
X(qubits)
ctrl(qubits, X)(auxiliar)
X(qubits)
H(qubits)
qulib.draw(gate=difusor_2, num_qubits=(3, 1), output="mpl")
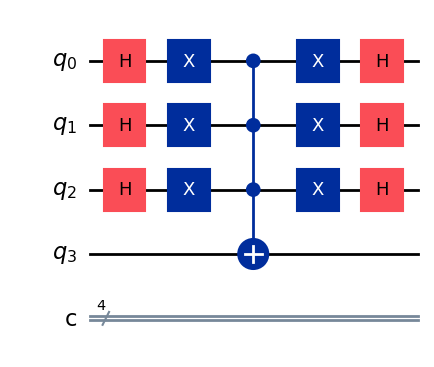
Além de facilitar a construção de algumas operações quânticas, a estrutura with around() também permite reduzir o número de qubits de controle em certas operações.
No exemplo abaixo, utilizamos with around() para definir uma porta SWAP e, em seguida, empregamos essa mesma porta para implementar uma porta de Fredkin, que é essencialmente uma versão controlada da SWAP.
Note que, no circuito abaixo, há menos qubits de controle em comparação com o exemplo anterior da porta de Fredkin.
def meu_swap_op(a, b):
with around(CNOT, a, b):
CNOT(b, a)
def fredkin_op(a, b, c):
ctrl(a, meu_swap_op)(b, c)
qulib.draw(gate=fredkin_op, num_qubits=(1, 1, 1), output="mpl")
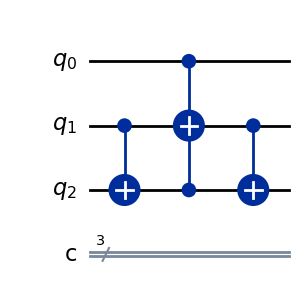
Alterando o Estado de Controle#
Por padrão, as operações quânticas são aplicadas apenas quando os qubits de controle estão no estado \(\ket{1}\). No entanto, em certos casos, precisamos alterar esse comportamento. Para isso, podemos usar a função ket.lib.flip_to_control() em conjunto com a instrução with around() para mudar o estado de controle de uma operação quântica.
O exemplo abaixo ilustra esse uso, onde queremos aplicar operações condicionais de acordo com os dados carregados. Neste exemplo, as operações condicionais são aplicadas nos qubits qubits com base nos dados carregados, e em seguida o emaranhamento é removido condicionalmente de acordo com esses mesmos dados.
processo = Process()
# Aloca qubits
qubits = processo.alloc(8)
aux = processo.alloc(2)
# Dados para processamento
dados = [11, 22, 33, 44]
# Aplica a Hadamard no registrador auxiliar
H(aux)
# Aplica as operações condicionais com base nos dados
for i, dado in enumerate(dados):
with around(qulib.flip_to_control(i), aux):
with control(aux):
for state, qubit in zip(f"{dado:0{len(qubits)}b}", qubits):
if state == "1":
X(qubit)
print("Dados carregados:")
display(dump(qubits + aux).show(f"i{len(qubits)}"))
# Remove o emaranhamento condicionalmente com base nos dados
for i, dado in enumerate(dados):
with around(qulib.flip_to_control(dado), qubits):
with control(qubits):
for state, qubit in zip(f"{i:0{len(aux)}b}", aux):
if state == "1":
X(qubit)
print("Emaranhamento removido condicionalmente:")
display(dump(qubits + aux).show(f"i{len(qubits)}"))
Dados carregados:
Emaranhamento removido condicionalmente:
Exercício: Implementando Portas Quânticas com with around#
Neste exercício, sua tarefa é utilizar a instrução with around() para reimplementar as portas lógicas quânticas RXX(), RYY() e RZZ(). Use como base para a reimplementação o circuito quântico de decomposição de cada porta.
Show code cell source
fig = qulib.draw(gate=RXX(3.141592654), num_qubits=(1, 1), output="mpl")
fig.suptitle("RXX Gate")
fig
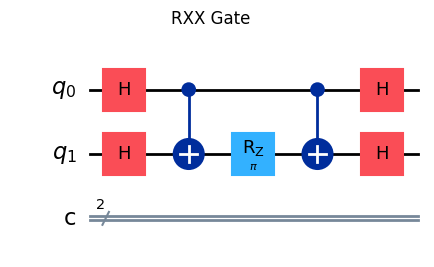
def porta_rxx(theta: float, qubits: Quant):
# Implemente a portas RXX(ϴ)
...
qulib.draw(gate=porta_rxx, num_qubits=(2,), args=(3.141592654,), output="mpl")
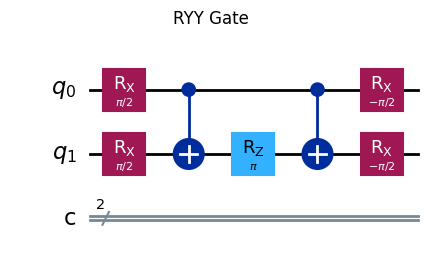
Show code cell source
fig = qulib.draw(gate=RYY(3.141592654, None, None), num_qubits=(1, 1), output="mpl")
fig.suptitle("RYY Gate")
fig
def porta_ryy(theta: float, qubits: Quant):
# Implemente a portas RYY(ϴ)
...
qulib.draw(gate=porta_ryy, num_qubits=(2,), args=(3.141592654,), output="mpl")
Show code cell source
fig = qulib.draw(gate=RZZ(3.141592654, None, None), num_qubits=(1, 1), output="mpl")
fig.suptitle("RZZ Gate")
fig
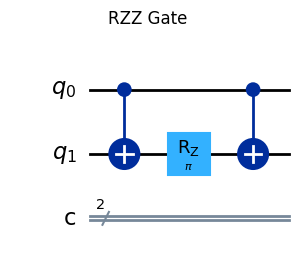
def porta_rzz(theta: float, qubits: Quant):
# Implemente a portas RZZ(ϴ)
...
qulib.draw(gate=porta_rzz, num_qubits=(2,), args=(3.141592654,), output="mpl")
Medidas#
Após realizar os cálculos na computação quântica, é necessário extrair os resultados para o ambiente clássico. Isso é feito por meio de medidas nos qubits. Nesta seção, exploraremos diferentes formas de medir qubits no Ket.
Extrair o Estado Quântico#
Ao simularmos um computador quântico, como fazemos neste capítulo, não estamos restritos às limitações da mecânica quântica. Assim, podemos extrair todo o estado quântico do simulador para manipulá-lo dentro do Python. Para isso, utilizamos a função dump(), que retorna uma instância de QuantumState.
Com o objeto QuantumState, é possível iterar sobre o estado quântico usando o atributo states. Neste atributo, o estado quântico é representado por um dicionário que mapeia o estado da base, representado por um número inteiro (int), para sua amplitude de probabilidade associada, representada por um número complexo (complex).
Aviso
A extração do QuantumState só é possível quando estamos em um ambiente simulado. Além disso, o QuantumState não tem a capacidade de representar estados mistos. Portanto, se o QuantumState representar um qubit entrelaçado com um qubit que não pertence ao mesmo QuantumState, a representação não será completa.
Tendo isso em mente, o uso da função dump() é uma ótima maneira de testar e debugar uma execução quântica. No entanto, não é recomendado substituir uma medida por esta abordagem.
Além do atributo states, é possível acessar o atributo probabilities para obter as probabilidades de medida. Também podemos utilizar o método sample() para simular uma amostragem a partir do QuantumState.
Abaixo, seguem exemplos de como utilizar a função dump() para extrair o estado quântico e iterar sobre ele através do atributo states.
processo = Process()
qubits = processo.alloc(2)
# prepara estado de Bell
cat(kron(H, I), CNOT)(*qubits)
estado_quântico = dump(qubits)
for estado, amplitude in estado_quântico.states.items():
print(f"{amplitude} |{estado}⟩")
(0.7071067811865476+0j) |0⟩
(0.7071067811865476+0j) |3⟩
Uma maneira alternativa de exibir o estado quântico é utilizando o método show() da classe QuantumState.
estado_quântico.show()
Medição de Qubits#
A função measure() é utilizada para medir qubits na base computacional, resultando em um objeto do tipo Measurement. Após a medição, o estado do qubit colapsa para o estado correspondente à medida realizada. Para extrair o resultado da medida, basta acessar o atributo value, o qual retorna um número inteiro sem sinal. É importante observar que o qubit de índice 0 corresponde ao bit de maior magnitude no resultado final. Portanto, a medição dos qubits \(\ket{\texttt{xyz}}\) resulta no número binário \(\texttt{0b}\texttt{xyz}\).
Abaixo está um exemplo de uso da função measure(). Neste exemplo, estamos medindo o primeiro qubit após a preparação do estado de Bell e exibindo o resultado da medida.
processo = Process()
qubits = processo.alloc(2)
# Preparando o estado de Bell
cat(kron(H, I), CNOT)(*qubits)
print("Estado quântico antes da medida")
display(dump(qubits).show())
medida = measure(qubits[0])
print("Resultado da medida do primeiro qubit:", medida.value)
print("Estado quântico após o colapso")
display(dump(qubits).show())
Estado quântico antes da medida
Resultado da medida do primeiro qubit: 0
Estado quântico após o colapso
Exercício: Medidas em Outras Bases#
Os computadores quânticos normalmente realizam medidas apenas na base computacional (base Z). No entanto, aplicando algumas operações quânticas, é possível realizar medidas em outras bases. Neste exercício, exploraremos medidas nas bases X e Y.
Medidas na Base X (Hadamard):
Na base X, também conhecida como base de Hadamard, a medida de um qubit no estado \(\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\) retorna 0, e a medida no estado \(\frac{1}{\sqrt{2}}(\ket{0}-\ket{1})\) retorna 1. Implemente as rotações necessárias nos qubits para efetuar uma medida na base computacional usando a função measure().
def medir_x(qubit: Quant) -> int: ...
def verificar_medir_x():
processo = Process()
a, b = processo.alloc(2)
X(b)
H(a + b)
assert medir_x(a) == 0
assert medir_x(b) == 1
print("Verificação concluída com sucesso")
# verificar_medir_x()
Medidas na Base Y:
Na base Y, a medida de um qubit no estado \(\frac{1}{\sqrt{2}}(\ket{0}+i\ket{1})\) retorna 0, e a medida no estado \(\frac{1}{\sqrt{2}}(\ket{0}-i\ket{1})\) retorna 1. Implemente as rotações necessárias nos qubits para efetuar uma medida na base computacional usando a função measure().
def medir_y(qubit: Quant) -> int: ...
def verificar_medir_y():
processo = Process()
a, b = processo.alloc(2)
X(b)
S(H(a + b))
assert medir_y(a) == 0
assert medir_y(b) == 1
print("Verificação concluída com sucesso")
# verificar_medir_y()
Amostragem de Qubits#
Muitos algoritmos quânticos dependem não apenas de uma medida exata, mas de uma distribuição de probabilidades. Portanto, é necessário executar várias medições em vez de apenas uma. Muitos computadores quânticos implementam esse comportamento, e o Ket oferece a função sample(), que retorna uma instância de Samples com os resultados das medições. Para acessar o resultado, basta ler o atributo value, que retorna um dicionário mapeando o estado medido ao número de vezes que esse estado foi observado.
Atenção
Nos simuladores padrão do Ket o estado quântico não é colapsado após a chamada da função sample(), e os qubits permanecem disponíveis para outras operações. No entanto, esse comportamento não é garantido em computadores quânticos reais, onde os qubits normalmente se tornam indisponíveis após a medição.
A seguir, apresentamos um exemplo de uso da função sample():
processo = Process()
qubits = processo.alloc(2)
# Preparando o estado de Bell
cat(kron(H, I), CNOT)(*qubits)
estado_quântico = dump(qubits)
print("Estado quântico")
display(dump(qubits).show("i"))
medida = sample(qubits)
print("Resultado das medidas:", medida.value)
Estado quântico
Resultado das medidas: {0: 1022, 3: 1026}

